UNIVERSITY COLLEGE LONDON
代写Engineering Sciences Assignment Release Date: 2nd October 2019•Assignment Hand-in Date: 16th October 2019 at 11.55am•Format: Problems
Faculty of Engineering Sciences
Department of Computer Science
COMP0036: LSA – Assignment 2
Dr. Dariush Hosseini ([email protected])
Overview Engineering Sciences
- Assignment Release Date: 2nd October2019
- AssignmentHand-in Date: 16th October 2019 at 55am
- Format:Problems
Guidelines 代写Engineering Sciences
- You should answer all THREE
- Note that not all questions carry equal
- You should submit your final report as a pdf using Turnitin accessed via themodule’s Moodle page.
- Within your report you should begin each question on a newpage.
- You should preface your report with a single page containing, on twolines:
- The module code:‘COMP0036’
- The assignment title: ‘LSA – Assignment2’
- Your report should be neat andlegible.代写Engineering Sciences
You are strongly advised to use LATEX to format the report, however this is not a hard requirement, and you may submit a report formatted with the aid of another system, or even a handwritten report, provided that you have converted it to a pdf (see above).
- Pleaseattempt to express your answers as succinctly as
- Please note that if your answer to a question or sub-question is illegible orincomprehen- sible to the marker then you will receive no marks for that question or sub-question.代写Engineering Sciences
- Please remember to detail your working, and state clearly any assumptions which you make.
- Failure to adhere to any of the guidelines may result in question-specific deduction of marks. If warranted these deductions may be punitive.

1.Assumean unlabelled dataset, .x(i) ∈ RmΣn, with sample mean, x = 1 Σn 代写Engineering Sciences
x(i), and an orthonormal basis set u[j] ∈ Rm d j=1, where d < m.
We have investigated the ‘Projected Variance Maximisation’ approach to PCA in which we are interested in finding the d-dimensional subspace spanned by .u[j] ∈ Rm|u[i] · u[j] = δij ∀i, jΣd
for which the sum of the sample variance of the data projected onto this subspace is max-imised.代写Engineering Sciences
This leads to a formulation of the PCA problem as:
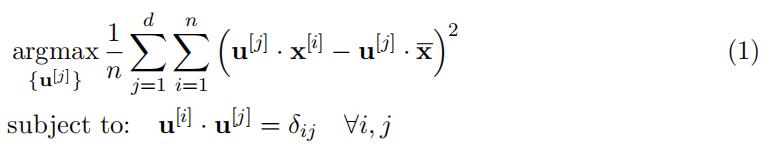
However there are several other approaches to PCA. One is the ‘Reconstruction Error Minimisation’ approach.Engineering Sciences代写
Here we are interested in finding the d-dimensional subspace spanned by .u[j]Σd
which minimises the reconstruction error, i.e.:
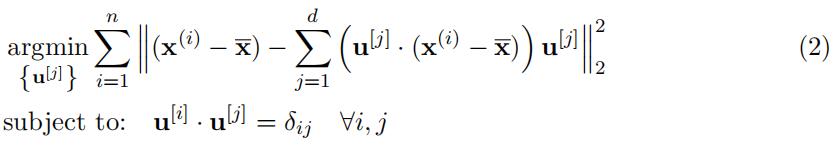
(a) [6 marks]
Show that problems (1) and (2) are equivalent.
(b) [4 marks]
In each analysis we were careful to centre our input data by effectively subtracting off the mean. Why is it important to centre the data in this way?
(c) [6 marks]代写Engineering Sciences
Show that we can re-write the objective of problem (1) as follows, and provide an expression for the matrix S:

(d) [4 marks]
If we were to replace S with the sample correlation matrix and then proceed to perform PCA with this objective, under what circumstances would this form of PCA differ from the covariance matrix version?代写Engineering Sciences
2.Assume a set of unlabelledpoints, {x(i)|Rd}n, which we wish to separate into k clusters.代写Engineering Sciences
We wish to use a ‘Spherical’ Gaussian Mixture Model (GMM) for this clustering task. Here we assume that each point has an unknown, latent, cluster assignment associated with it, z ∈ {1, …, k}, which is the outcome of a multinomial random variable, Z:
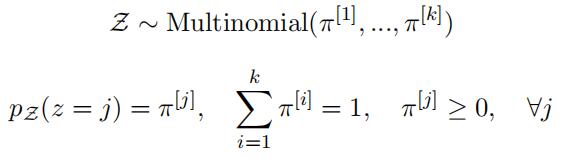
Furthermore, contingent on the cluster assignment, z, we assume that each point, x, is the outcome of a Gaussian random variable, X :
X |(z = j) ∼ N (x|µ , Σ )
Where:
µ[j] ∈ Rd is the mean associated with cluster j, and;
Σ[j] = sI is the covariance associated with each cluster j.
Here s is a constant, and I denotes the d × d identity matrix.Engineering Sciences1代写
(a) [6 marks]
Give an expression for the log likelihood of the dataset, {x(i)}n
in terms of s and {µ[j], π[j]}k .
(b) [5 marks]代写Engineering Sciences
We wish to maximise this expression subject to the usual constraints using the EM algorithm.
Give an expression for the responsibilities, γi[j], in this case.
(c) [8 marks]
Explain why, as s → 0, the solution we generate from the spherical GMM EM clustering algorithm will tend towards the solution we would generate from the k-means clustering algorithm.Engineering Sciences1代写
(d) [3 marks]
Describe and explain the form of the boundary which discriminates between clusters in this case.
(e) [3 marks]
Now consider the more usual GMM EM clustering algorithm, in which we assume that the covariances, Σ[j] > 0, are no longer constrained to take the isotropic form which we assumed earlier and are in general distinct ∀j.Engineering Sciences代写
Describe and explain the form of the boundary which discriminates between clusters in this case in general.
3.(a) [4marks]
Explain the importance of the Representer Theorem?
(b) [3 marks]
Consider the A1-regularised Logistic regression optimisation problem:
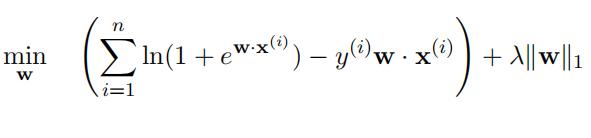
Here:
{x(i), y(i)}n=1
represents a set of training data, where x ∈ Rm are input attributes,
while y ∈ {0, 1} is the output label;代写Engineering Sciences
w ∈ Rm is the weight vector of the linear discriminant which we seek, and;
λ > 0 is some constant.
Is this problem susceptible to the kernel trick? Explain.
(c) [4 marks]
Consider the following clustering problem:
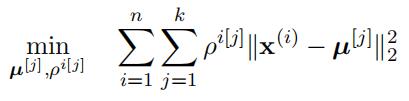
Here:
{x(i)}ni=1represents a set of unlabelled points, where x ∈ Rm are input attributes;
{µ[j] ∈ Rm}k represent the k cluster centroids, and;
{ρi[j] ∈ {0, 1}}n,k represent a set of assignment variables.代写Engineering Sciences
Let us seek to perform this optimisation using the k-means algorithm.
Is the M-step of this procedure susceptible to the kernel trick? Explain.
(d) [4 marks]
Assuming 2-dimensional input attributes, x = [x1, x2]T , what kernel function, κ, is associated with the following feature map, φ (express your answer in terms of vectordot products):
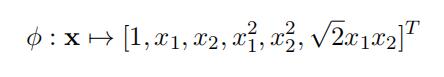
(e) [5 marks]代写Engineering Sciences
Assuming 1-dimensional input attributes, x, what feature map, φ : x ›→ φ(x), is associated with the following kernel, κ:
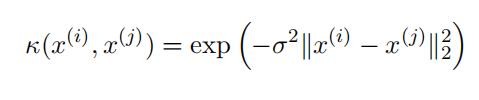

其他代写:考试助攻 计算机代写 java代写 algorithm代写 assembly代写 function代写paper代写 finance代写 web代写 编程代写 report代写 algorithm代写 数学代写 作业代写 代写CS作业 python代写 app代写 r代写
