Amsterdam School of Economics
Empirical Project – Group Assignment 1 (week 1) The Mincer Wage Equation
Aim:
The aim of this assignment is to familiarise students with the empirical application of ordinary least squares. Creating usable data files and doing proper econometric analysis is part of this.
Report:
Write in two pages A4 a compact analysis of the wage equation. Use the common structure: Title, Authors, Abstract. 1 Introduction. 2. Theoretical background and method. 3 Data 4 Results and preferred empirical model. 5. Conclusion. 6. Appendix (this is in addition to the two pages and should contain all the background material and regressions, specification tests etc.
Submit a pdf version of this report before Monday 11 June 9:00 (am) in Blackboard. Do not forget the names and student numbers of all group members.
Assessment:
This assignment will be marked out of 10. It is worth 10% of the final mark for the course ’Empirical Project’.
Literature:
![]() Heij, C., Boer, P. de, Franses, P.H., Kloek, T. and Dijk, H.K. van, 2004, Econometric Methods with Applications in Business and Economics, Oxford University Press;
Heij, C., Boer, P. de, Franses, P.H., Kloek, T. and Dijk, H.K. van, 2004, Econometric Methods with Applications in Business and Economics, Oxford University Press;
Artikelen:
![]() Björklund, A. and Kjellström, J., 2002, Estimating the return to investments on edu- cation: how useful is the standard Mincer equation?, Economics of Education Review, vol. 21, pp. 195-210.
Björklund, A. and Kjellström, J., 2002, Estimating the return to investments on edu- cation: how useful is the standard Mincer equation?, Economics of Education Review, vol. 21, pp. 195-210.
![]() Harmon, C., and Walker, I., 1995, Estimates of the economic return to schooling for the United Kingdom, American Economic Review, vol.85, pp.1278-1286. (N.B. Dit artikel wordt in deze opdracht enkel aangehaald en wordt nader beschouwd in de opdracht van volgende week.)
Harmon, C., and Walker, I., 1995, Estimates of the economic return to schooling for the United Kingdom, American Economic Review, vol.85, pp.1278-1286. (N.B. Dit artikel wordt in deze opdracht enkel aangehaald en wordt nader beschouwd in de opdracht van volgende week.)
![]() Lemieux, T., 2006, The "Mincer Equation" thirty years after Schooling, Experience, and Earnings, Chapter 11 of Jacob Mincer a Pioneer in Modern Labor Eonomics, Gross- bard, S. (ed.), Springer.1
Lemieux, T., 2006, The "Mincer Equation" thirty years after Schooling, Experience, and Earnings, Chapter 11 of Jacob Mincer a Pioneer in Modern Labor Eonomics, Gross- bard, S. (ed.), Springer.1
Data:
![]() Description: Cross sections of the American "Current Population Survey" (CPS), years 2003-2014.
Description: Cross sections of the American "Current Population Survey" (CPS), years 2003-2014.
• Further info: http://www.nber.org/cps
• Data download: http://www.nber.org/data/current-population-survey-data.html
![]() Specific data for the assignment: There are ten data files (cps2004.dta – cps2013.dta) available on Blackboard. Each group analyses one year based on the last digit of the of the oldest group member. So e.g. if the last digit is 5 then this group uses cps2009.dta. All data files contain about 8000 observations.
Specific data for the assignment: There are ten data files (cps2004.dta – cps2013.dta) available on Blackboard. Each group analyses one year based on the last digit of the of the oldest group member. So e.g. if the last digit is 5 then this group uses cps2009.dta. All data files contain about 8000 observations.
|
Version |
Use year |
|
0 |
2004 |
|
1 |
2005 |
|
2 |
2006 |
|
3 |
2007 |
|
4 |
2008 |
|
5 |
2009 |
|
6 |
2010 |
|
7 |
2011 |
|
8 |
2012 |
|
9 |
2013 |
A limited number of variables corresponding to those in Björklund en Kjellström (2002) have been selected. There has not been made a selection based on gender (in contrast with Björklund en Kjellström, 2002) and there is additional information about ethnicity of the respondents. We have the following variables:
• hwage = hourly wage in $;
• female = dummy equal to 1 for woman;
• educ = education in years (approximate, see below);
• leduc = level of schooling (precise definition given below);
• age = age in years;
• lexp = labour market experience (approximate, see below);
1Download: http://link.springer.com/chapter/10.1007/0-387-29175-X_11#page-1
• etngroup = ethnic group (precise definition given below).
Specific information on variables:
• leduc
————————————————-
leduc – educational |
attainment | code educ
——————————–+—————-
|
Less than 1st grade |
| |
31 |
1 |
|
1st,2nd,3rd,or 4th grade |
| |
32 |
2.5 |
|
5th or 6th grade |
| |
33 |
5.5 |
|
7th and 8th grade |
| |
34 |
7.5 |
|
9th grade |
| |
35 |
9 |
|
10th grade |
| |
36 |
10 |
|
11th grade |
| |
37 |
11 |
|
12th grade no diploma |
| |
38 |
12 |
|
High school graduate – high |
| |
39 |
12 |
|
Some college but no degree |
| |
40 |
13 |
|
Associate degree in college – |
| |
41 |
14 |
|
Associate degree in college – |
| |
42 |
14 |
|
Bachelor's degree (for |
| |
43 |
16 |
|
Master's degree (for |
| |
44 |
18 |
|
Professional school degree (for |
| |
45 |
24 |
|
Doctorate degree (for |
| |
46 |
24 |
————————————————-
![]() educ is based on leduc. De duration is based on the nominal duration to attain a certain educational level.
educ is based on leduc. De duration is based on the nominal duration to attain a certain educational level.
• lexp = age – 6 – educ
• etngroup
————————————–
etngroup – etnical group | code
————————–+———–
|
White only |
| |
1 |
|
Black only |
| |
2 |
|
American Indian, |
| |
3 |
|
Asian only |
| |
4 |
|
Hawaiian/Pacific Islander |
| |
5 |
|
White-Black |
| |
6 |
|
White-AI |
| |
7 |
|
White-Asian |
| |
8 |
|
White-HP |
| |
9 |
|
Black-AI |
| |
10 |
|
Black-Asian |
| |
11 |
|
Black-HP |
| |
12 |
|
AI-Asian |
| |
13 |
|
AI-HP |
| |
14 |
|
Asian-HP |
| |
15 |
|
White-Black-AI |
| |
16 |
|
White-Black-Asian |
| |
17 |
|
White-Black-HP |
| |
18 |
|
White-AI-Asian |
| |
19 |
|
White-AI-HP |
| |
20 |
|
White-Asian-HP |
| |
21 |
|
Black-AI-Asian |
| |
22 |
|
White-Black-AI-Asian |
| |
23 |
|
White-AI-Asian-HP |
| |
24 |
??????????????????????????| 25
Other 4 or 5 race comb. | 26
————————————–
Statistical tests:
If you carry out a test, you should do so comprehensively. Specify null- and alternative hypotheses, indicate how the teststatistic is calculated, give its (approximate) distribution under the null, give its (realised) value, compare with the critical value, and draw your conclusion.
Motivate and substantiate your answer! Assignment details
You will investigate and replicated parts of Björklund en Kjellström (2002) using US data for
a single year. They use multiple years and restrict themselves to males. We shall investigate the gender gap. Starting point is the Mincerian wage equation which in its basic form is given by:
log(y) = β0 + β1s + β2x + β3x2 + ε,
with s = years of schooling and x =years of labour market experience.
In writing the report you can use the following suggestions. Carry out these suggestions where appropriate, but only report relevant results ieither in the main text or the appendix. Do NOT make the appendix a list of all the things suggested here.
1. Put the information in a format that is useful for you. The data are available in Stata-format. To put it in another format do the following
(a) Open STATA and open the data file (with extension .dta
(b) Export the data to the desired format using “File – Export" . The .xls(x) or .csv file types can be read by excel ad EViews. Some packages, like Gretl, EViews, R, can read Sata files directly without transforming. An alternative is using the package StatTransfer.
2. You now have the raw data. You should check that the data are correct (do not contain obvious errors) and are suitable or your investigation.
(a) Make a histogram of houly wage and assess whether it could be normally dis- tributed (test!) Decide whether wage below 2$/h or above 90 $/h should be included in your sample. What are the mean, mode, and standard deviation?
(b) Consider the other variables and present a table with summary statistics (in the appendix) Are there strange values?
(c) Dropping observations can be problematic. Why? Is it different when observations are dropped on the basis of explanatory variables or on dependent variables?
3. Reproduce some of the results of Björklund en Kjellström (2002). This means that you should restrict yourselves to males and natural log of hourly wage.
(a) Reproduce Table 1 and Table 2 for your year and consider the differences.
(b) Reproduce the columns III in Table 4. These columns are based on natural loga- rithms and the other columns relate to Box-Cox transformed data. Can you test whether this result is significantly different from (a)?
(c) Reproduce Table 5 with log(hwage) as dependent variable (so no Box-Cox trans- formations) Test if it is appropriate to add interaction effects and interpret the coefficients.
(d) Repeat (a)-(c) for females
4. Is there a significant difference between men and women. Consider models with dum- mies, rather than estimating separate equations for men and women.
5. Investigate the effect of ethnicity. Is it significant?
6. Which other variables do you think should be included in the Mincerian wage equation? What are the consequences of their non-availability in the data set?
7. Test for non linearity in the model. (Note that the dependent variable can be in logs, Box-Cox transformed, or not transformed).
8. Does it make sense to test for serial correlation and heteroskedasticity?
(a) If it does, check this possible specification error using different tests. Comment. Pay special attention if different tests give conflicting results.
(b) Take appropriate action if the specification of the model is rejected.
(c) Is there a significant effect of ethnicity?
9. For the correct specification and interpretation of the model it is important that the explanatory variables are exogenous. Exogeneity of schooling is questionable. An important argument is ability bias, as highlighted by e.g. Harmon en Walker (1995) which we will consider next week. Intelligence is difficult to measure and usually missing from the data, but is an obvious factor in wage. This missing variable is likely to be correlated with variables in the model.
(a) Argue the sign of bias that result of this missing variable.
(b) Does your bias expression in (a) agree with the results in Harmon en Walker (1995)?
(c) The only potential instrument to be used is age. Is this valid and useful?
作业答案:
Stata code
clear all
cd E:\desktop\xieshou
use 180607empiricalproject
*** set time series
split (date) ,g(part) p("/")
forv j = 1/3 {
replace part`j' = "0" + part`j' if length(part`j') < 2
}
gen datequarter= part1+part2+part3
gen dateq=date(datequarter,"YMD")
format dateq %td
gen quarterdate=qofd(dateq)
format quarterdate %tq
tsset quarterdate, quarterly
label variable dloggdp "Income Growth Rate"
label variable dlognd "Consumption Growth Rate"
label variable dlogdj "Stock market Growth Rate"
*** Q1
*a
gen loggdp=log(gdp)
gen lognd=log(nd)
gen logdj=log(dj)
gen dloggdp=d.loggdp
gen dlognd=d.lognd
gen dlogdj=d.logdj
*b
sum dloggdp dlognd dlogdj, detail
*c
corr dloggdp dlognd dlogdj
*d
corrgram dloggdp,lag(6)
corrgram dlognd,lag(6)
corrgram dlogdj,lag(6)
*e
scatter dlognd dloggdp
scatter dlognd dlogdj
*** Q2
reg dlognd L.dloggdp L.dlogdj L.dlognd
est sto m1
test (L.dlogdj =0) (L.dloggdp =0)
reg dlognd L.dlognd L2.dlognd L3.dlognd L4.dlognd
est sto m2
test (L2.dlognd=0) (L3.dlognd=0) (L4.dlognd=0)
reg dlognd L.dlognd L.dloggdp L2.dloggdp L3.dloggdp L4.dloggdp
est sto m3
test (L.dloggdp=0) (L2.dloggdp=0) (L3.dloggdp=0) (L4.dloggdp=0)
reg dlognd L.dlognd L.dlogdj L2.dlogdj L3.dlogdj L4.dlogdj
est sto m4
test (L.dlogdj=0) (L2.dlogdj=0) (L3.dlogdj=0) (L4.dlogdj=0)
esttab m1 m2 m3 m4 using "consumption.rtf", replace label varwidth(26) cells(b(star fmt(4)) se(par fmt(4))) modelwidth(8) star(* 0.10 ** 0.05 *** 0.01) ///
se stats(r2 N, labels("R-Square" "Number of Observation")) ///
varlabels(_cons Constant)
*** Q3
*a
reg dloggdp L.dloggdp L2.dloggdp L3.dloggdp L4.dloggdp
est sto m5
test (L.dloggdp=0) (L2.dloggdp=0) (L3.dloggdp=0) (L4.dloggdp=0)
reg dloggdp L.dlognd L2.dlognd L3.dlognd L4.dlognd
est sto m6
test (L.dlognd=0) (L2.dlognd=0) (L3.dlognd=0) (L4.dlognd=0)
reg dloggdp L.dlogdj L2.dlogdj L3.dlogdj L4.dlogdj
est sto m7
test (L.dlogdj=0) (L2.dlogdj=0) (L3.dlogdj=0) (L4.dlogdj=0)
esttab m5 m6 m7 using "consumptionQ3a.rtf", replace label varwidth(26) cells(b(star fmt(4)) se(par fmt(4))) modelwidth(8) star(* 0.10 ** 0.05 *** 0.01) ///
se stats(r2 N, labels("R-Square" "Number of Observation")) ///
varlabels(_cons Constant)
*b
reg dlognd L.dlogdj L2.dlogdj L3.dlogdj L4.dlogdj
predict predlognd, xb
est sto m8
reg dloggdp L.dlogdj L2.dlogdj L3.dlogdj L4.dlogdj
predict predloggdp, xb
est sto m9
esttab m8 m9 using "consumptionQ3b.rtf", replace label varwidth(26) cells(b(star fmt(4)) se(par fmt(4))) modelwidth(8) star(* 0.10 ** 0.05 *** 0.01) ///
se stats(r2 N, labels("R-Square" "Number of Observation")) ///
varlabels(_cons Constant)
label variable predloggdp "Predicted Income Growth Rate"
label variable predlognd "Predicted Consumption Growth Rate"
scatter predlognd predloggdp
*c
ivreg dlognd (dloggdp=dlogdj)
est sto m10
esttab m10 using "consumptionQ3c.rtf", replace label varwidth(26) cells(b(star fmt(4)) se(par fmt(4))) modelwidth(8) star(* 0.10 ** 0.05 *** 0.01) ///
se stats(r2 N, labels("R-Square" "Number of Observation")) ///
varlabels(_cons Constant)
Report:
Q1
a)
In Stata
b)
|
Variable |
Obs |
Mean |
Std. Dev. |
Min |
Max |
Median |
|
GDP |
243 |
0.005223 |
0.009801 |
-0.03121 |
0.036052 |
0.005151 |
|
ND |
243 |
0.007964 |
0.00519 |
-0.00934 |
0.024995 |
0.008044 |
|
DJ |
243 |
0.009407 |
0.057764 |
-0.24608 |
0.161582 |
0.011949 |
c)
|
GDP |
ND |
DJ |
|
|
GDP |
1 |
||
|
ND |
0.4438 |
1 |
|
|
DJ |
0.1933 |
0.2677 |
1 |
d)
|
GDP |
ND |
DJ |
|
|
LAG |
AC |
AC |
AC |
|
1 |
0.3368 |
0.1931 |
0.3227 |
|
2 |
0.1792 |
0.1645 |
0.0569 |
|
3 |
-0.0299 |
0.1406 |
0.0189 |
|
4 |
-0.1119 |
-0.0014 |
0.0083 |
|
5 |
-0.1704 |
-0.0388 |
-0.0373 |
|
6 |
-0.0937 |
-0.0052 |
-0.0731 |
e)
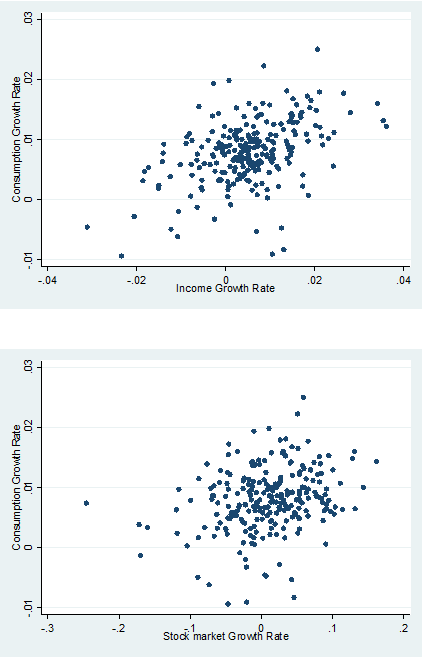
Q2
The regression results are as follows. We can see that the one period lagged income and wealth (stock market index) growth rate have predictive power for the consumption growth rate. The two to four period lagged consumption growth rates also have predictive power for the consumption growth rate. The one to four period lagged income growth rate do not have significant predict power for the consumption growth rate (the p-value is at the margin of 5% significant level). The one to four period lagged wealth growth rate have predictive power for the consumption growth rate. According to Hall (1978), the pure life cycle-permanent income hypothesis claims that Ct cannot be predicted by any variable dated t-1 or earlier other than Ct-1. The empirical result does not support the hypothesis.
|
(1) |
(2) |
(3) |
(4) |
|
|
Consumption Growth Rate |
Consumption Growth Rate |
Consumption Growth Rate |
Consumption Growth Rate |
|
|
b/se |
b/se |
b/se |
b/se |
|
|
L.Income Growth Rate |
0.1059*** |
0.1001*** |
||
|
(0.0363) |
(0.0385) |
|||
|
L2.Income Growth Rate |
0.0360 |
|||
|
(0.0366) |
||||
|
L3.Income Growth Rate |
-0.0326 |
|||
|
(0.0364) |
||||
|
L4.Income Growth Rate |
0.0036 |
|||
|
(0.0348) |
||||
|
L.Stock market Growth Rate |
0.0143** |
0.0167*** |
||
|
(0.0057) |
(0.0059) |
|||
|
L2.Stock market Growth Rate |
-0.0042 |
|||
|
(0.0062) |
||||
|
L3.Stock market Growth Rate |
0.0146** |
|||
|
(0.0061) |
||||
|
L4.Stock market Growth Rate |
-0.0005 |
|||
|
(0.0058) |
||||
|
L.Consumption Growth Rate |
0.0626 |
0.1510** |
0.0900 |
0.1312* |
|
(0.0700) |
(0.0653) |
(0.0720) |
(0.0668) |
|
|
L2.Consumption Growth Rate |
0.1486** |
|||
|
(0.0642) |
||||
|
L3.Consumption Growth Rate |
0.1016 |
|||
|
(0.0644) |
||||
|
L4.Consumption Growth Rate |
-0.0653 |
|||
|
(0.0634) |
||||
|
Constant |
0.0067*** |
0.0053*** |
0.0067*** |
0.0067*** |
|
(0.0006) |
(0.0009) |
(0.0006) |
(0.0006) |
|
|
Joint Test P-value for coefficients other than Ct-1 |
0.0004 |
0.0268 |
0.0511 |
0.0080
|
|
R-Square |
0.0986 |
0.0728 |
0.0739 |
0.0909 |
|
Number of Observation |
242.0000 |
239.0000 |
239.0000 |
239.0000 |
Q3
a)
The regressions of GDP growth on lagged values of GDP growth, lagged values of consumption growth and lagged stock market growth are as follows (four periods lags are used)
|
(1) |
(2) |
(3) |
|
|
Income Growth Rate |
Income Growth Rate |
Income Growth Rate |
|
|
b/se |
b/se |
b/se |
|
|
L.Income Growth Rate |
0.3066*** |
||
|
(0.0651) |
|||
|
L2.Income Growth Rate |
0.1321* |
||
|
(0.0677) |
|||
|
L3.Income Growth Rate |
-0.0952 |
||
|
(0.0676) |
|||
|
L4.Income Growth Rate |
-0.0943 |
||
|
(0.0648) |
|||
|
L.Consumption Growth Rate |
0.7896*** |
||
|
(0.1167) |
|||
|
L2.Consumption Growth Rate |
0.3298*** |
||
|
(0.1146) |
|||
|
L3.Consumption Growth Rate |
-0.1074 |
||
|
(0.1150) |
|||
|
L4.Consumption Growth Rate |
-0.0646 |
||
|
(0.1132) |
|||
|
L.Stock market Growth Rate |
0.0508*** |
||
|
(0.0108) |
|||
|
L2.Stock market Growth Rate |
0.0252** |
||
|
(0.0114) |
|||
|
L3.Stock market Growth Rate |
0.0072 |
||
|
(0.0114) |
|||
|
L4.Stock market Growth Rate |
0.0102 |
||
|
(0.0107) |
|||
|
Constant |
0.0039*** |
-0.0024 |
0.0044*** |
|
(0.0008) |
(0.0015) |
(0.0006) |
|
|
R-Square |
0.1413 |
0.2094 |
0.1561 |
|
Number of Observation |
239.0000 |
239.0000 |
239.0000 |
We can see that both the three groups of lagged variables have predictive power for GDP growth. I use choose the one to four lagged stock market growth rate as Xt-1 to forecast income growth. In this way, all the three variables (consumption, income, wealth) can be used in this question: lagged wealth variables used as IV, consumption and fitted income variables are used in the regression.
b)
The regression results are as follows
|
(1) |
(2) |
|
|
Consumption Growth Rate |
Income Growth Rate |
|
|
b/se |
b/se |
|
|
L.Stock market Growth Rate |
0.0193*** |
0.0508*** |
|
(0.0058) |
(0.0108) |
|
|
L2.Stock market Growth Rate |
-0.0025 |
0.0252** |
|
(0.0062) |
(0.0114) |
|
|
L3.Stock market Growth Rate |
0.0144** |
0.0072 |
|
(0.0061) |
(0.0114) |
|
|
L4.Stock market Growth Rate |
0.0014 |
0.0102 |
|
(0.0058) |
(0.0107) |
|
|
Constant |
0.0077*** |
0.0044*** |
|
(0.0003) |
(0.0006) |
|
|
R-Square |
0.0759 |
0.1561 |
|
Number of Observation |
239.0000 |
239.0000 |
The scatter plot of the fitted values from the above regressions is as follows
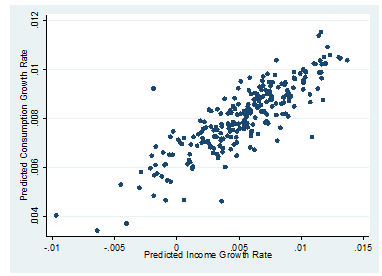
We can see that compared with Q1 e), the points are more concentrated for the fitted values. And the scatter plot of fitted points is more like a line with positive slope. If equation (1) is true, ![]() , so
, so![]()
Therefore, we should have ![]() .
.
From the scatter plot, we can see that the income growth rate and consumption growth rate are positively correlated, this provides a preliminary support for equation (1).
c)
The regression result is as follows
|
(1) |
|
|
Consumption Growth Rate |
|
|
b/se |
|
|
Income Growth Rate |
0.7333*** |
|
(0.2293) |
|
|
Constant |
0.0041*** |
|
(0.0013) |
|
|
Number of Observation |
243.0000 |
We can see that the coefficient on Income Growth Rate ![]() is 0.7333. The coefficient is highly significant (p value is below 1% level). The value of
is 0.7333. The coefficient is highly significant (p value is below 1% level). The value of ![]() is between 0 and 1, which tends to be consistent with the model’s setting. The result suggests that 73.33% of consumers simply consume their current income.
is between 0 and 1, which tends to be consistent with the model’s setting. The result suggests that 73.33% of consumers simply consume their current income.
代写CS&Finance|建模|代码|系统|报告|考试
编程类:C++,JAVA ,数据库,WEB,Linux,Nodejs,JSP,Html,Prolog,Python,Haskell,hadoop算法,系统 机器学习
金融类:统计,计量,风险投资,金融工程,R语言,Python语言,Matlab,建立模型,数据分析,数据处理
服务类:Lab/Assignment/Project/Course/Qzui/Midterm/Final/Exam/Test帮助代写代考辅导
天才写手,代写CS,代写finance,代写statistics,考试助攻
E-mail:[email protected] 微信:BadGeniuscs 工作时间:无休息工作日-早上8点到凌晨3点
如果您用的手机请先保存二维码到手机里面,识别图中二维码。如果用电脑,直接掏出手机果断扫描。

