第1节 课后习题
1.1 已知n+1个节点xi及yi=f(xi)(i=0,…,n),编写n次Lagrange差值与n次Newton差值的通用程序。然后根据给定的数据表:
|
x |
0.46 |
0.47 |
0.48 |
0.49 |
|
f(x) |
0.4846555 |
0.4937452 |
0.5027498 |
0.5116683 |
利用所编的通用程序计算f(0.485)
编程思想:
Lagrange差值公式:![]()
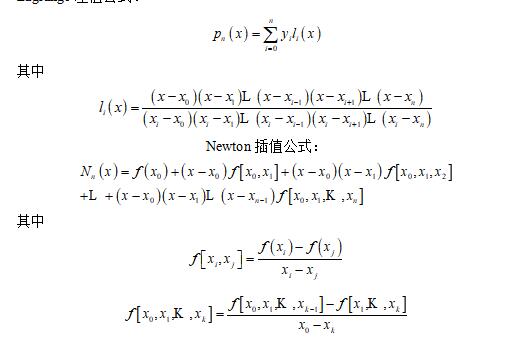
计算程序:
Lagrange差值通用程序:
function y=fun_test_1_1_Lagrange(x,x1,y1)
% Lagrange插值法
for nx=1:length(x)
for nx1=1:length(x1)
tempx=x1;
tempx(nx1)=[];
temp1=x(nx)-tempx;
temp2=x1(nx1)-tempx;
lx(nx1)=prod(temp1)/prod(temp2);
end
y(nx)=sum(y1.*lx);
end
Newton插值通用程序:
function y=fun_test_1_1_Newton(x,x1,y1)
% Newton插值法
for nx=1:length(x)
temp1=y1(1);
temp2=y1(2);
lk(1)=y1(1);
yk(1)=1;
for nx1=2:length(x1)-1
temp11=(temp2-temp1)/(x1(nx1)-x1(nx1-1));
temp2=(y1(nx1+1)-temp1)/(x1(nx1+1)-x1(nx1-1));
temp1=temp11;
lk(nx1)=temp1;
yk(nx1)=prod(x(nx)-x1(1:nx1-1));
end
y(nx)=sum(yk.*lk);
end
计算结果:
Lagrange差值:f(0.485)= 0.507219875
Newton差值:f(0.485)= 0.5072201875
1.2 已知n+1个等距节点xi=x0+ih及yi=f(xi)(i=0…,n),编写Newton向前插值和向后插值的通用程序,然后根据给定的数据:
|
x |
1.3 |
1.31 |
1.32 |
1.33 |
|
f(x) |
3.6021 |
3.7471 |
3.9033 |
4.0723 |
利用所编的通用程序分别计算f(1.305)和f(1.325).
编程思想:
向前查分符![]() :
:![]()
向后查分符![]() :
:![]()
取等距节点xi=x0+ih,yi=f(xi),
(1)Newton向前插值公式:
![]()
(2)Newton向后插值公式:
![]()
计算程序:
(1)向前差值通用程序
function y=test_1_2_forword(x,x0,h,y1)
% 牛顿向前差分
for nx=1:length(x)
temp1=y1(1);
temp2=y1(2);
lk(1)=1;
yk(1)=y1(1);
t=(x(nx)-x0)/h;
for nx1=2:length(y1)-1
lk(nx1)=prod(t-(0:nx1-2))/factorial(nx1-1);
temp1=temp2-temp1;
temp2=y1(nx1+1)-temp2;
yk(nx1)=temp1;
end
y(nx)=sum(yk.*lk);
end
(2)向后差分通用程序
function y=test_1_2_backword(x,x0,h,y1)
% 牛顿向前差分
for nx=1:length(x)
temp1=y1(end);
temp2=y1(end-1);
lk(1)=1;
yk(1)=y1(end);
t=(x(nx)-x0)/h;
for nx1=2:length(y1)-1
lk(nx1)=prod(t-(0:nx1-2))/factorial(nx1-1);
temp1=temp1-temp2;
temp2=temp2-y1(length(y1)-nx1);
yk(nx1)=temp1;
end
y(nx)=sum(yk.*lk);
end
主程序:
clear,clc
format long
x1=[1.3,1.31,1.32,1.33];
y1=[3.6021,3.7471,3.9033,4.0723];
x=[1.305,1.325];
%前插Newton插值
disp('前插Newton插值')
y=test_1_2_forword(x,1.3,0.01,y1)
%后插Newton插值
disp('后插Newton插值')
y=test_1_2_backword(x,1.33,0.01,y1)
计算结果:
(1)向前差分:
f(1.305)和f(1.325)分别为:3.6732和3.9856
(2)向后差分:
f(1.305)和f(1.325)分别为:3.7058和3.9926
1.3 给定函数![]() ,分别取n=5,10,20,在区间[-5,5]上取等距节点做n次Lagrange差值,画图给出n次Lagrange差值多项式的图像并与f(x)的图像进行比较。
,分别取n=5,10,20,在区间[-5,5]上取等距节点做n次Lagrange差值,画图给出n次Lagrange差值多项式的图像并与f(x)的图像进行比较。
编程思想:
与1.1相同。
计算程序:
clear,clc
format long
n=5;
fx=@(x)1./(1+x.^2);
x1=linspace(-5,5,n);
x=linspace(-5,5,1000);
%lagrange插值
y=fun_test_1_1_Lagrange(x,x1,fx(x1));
plot(x1,fx(x1),x,y)
计算结果:
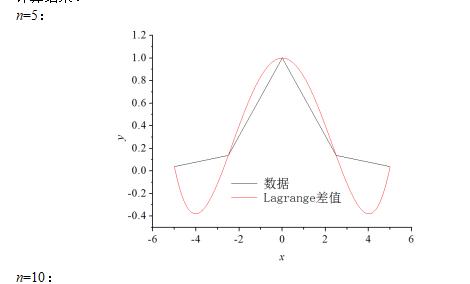
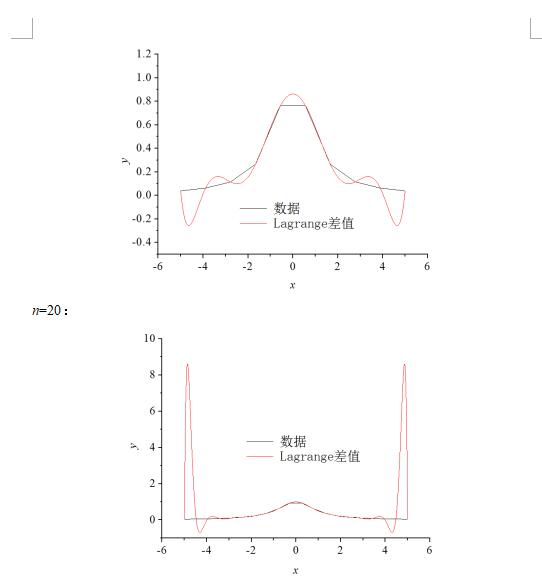
1.4 取n=20,利用![]() 给出所需数据在区间[-5,5]上取n+1个等距节点,分别作分段线性插值和分段三次Hermite插值,画图给出分段线性插值和分段三次Hermite插值多项式的图像,并与f(x)的图像进行比较,另外,以你的教学好的后三位构造[3.7,3.8]内的点xc,给出两种插值多项式在xc处的值。
给出所需数据在区间[-5,5]上取n+1个等距节点,分别作分段线性插值和分段三次Hermite插值,画图给出分段线性插值和分段三次Hermite插值多项式的图像,并与f(x)的图像进行比较,另外,以你的教学好的后三位构造[3.7,3.8]内的点xc,给出两种插值多项式在xc处的值。
编程思想:
分段三次Hermite插值公式:
分段线性插值:
![]()
计算程序:
分段三次Hermite插值公通用程序:
function y=fun_test_1_4_Hermite(xm,xn,f,df)
% 三次Hermite插值法
% x为插值点,x1和y1分别为已知数据的自变量和因变量
% dy为因变量的导数
for nx=1:length(xm)
x=xm(nx);
nn1=max(find(xn<=xm(nx)));
nn2=min(find(xn>=xm(nx)));
x0=xn(nn1);
x1=xn(nn2);
temp1=(1-2*(x-x0)/(x0-x1))*((x-x1)/(x0-x1))^2*f(nn1);
temp2=(x-x0)*((x-x1)/(x1-x0))^2*df(nn1);
temp3=(1-2*(x-x1)/(x1-x0))*((x-x0)/(x1-x0))^2*f(nn2);
temp4=(x-x1)*((x-x0)/(x0-x1))^2*df(nn2);
y(nx)=temp1+temp2+temp3+temp4;
end
分段线性插值通用程序:
function y=fun_test_1_4_line(xm,xn,f)
% 线性插值
for nx=1:length(xm)
x=xm(nx);
nn1=max(find(xn<=xm(nx)));
nn2=min(find(xn>=xm(nx)));
x0=xn(nn1);
x1=xn(nn2);
y(nx)=(x-x1)/(x0-x1)*f(nn1)+(x-x0)/(x1-x0)*f(nn2);
end
计算主程序:
clear,clc
format long
n=10;
fx=@(x)1./(1+x.^2);
dfx=@(x)-2*x./(1+x.^2).^2;
x1=linspace(-5,5,n+1);
y1=fx(x1);
x=linspace(-5,5,100);
yH=fun_test_1_4_Hermite(x,x1,fx(x1),dfx(x1))
plot(x1,fx(x1),x,yH,'p')
hold on
yL=fun_test_1_4_line(x,x1,fx(x1))
plot(x,yL,'-o')
计算结果:
分段三次Hermite插值和分段线性插值的f(3.7403)分别为:0.06666和0.06952.
