STA Assignment
代写统计学作业 Why do you see a difference in your calculation in part(a) and part(b)? And under whatcondition you expect these two numbers to be similar?
Question 1 (4 points)
In question 1 of assignment 1, you created all possible combinations(4096 of them) of samples of size (n=4) from this following population.
11, 12, 13, 14, 15, 16, 17, 18
Here is the code again that will produce 4096 different values of X-bar.
Even though we need sample size n to be large to apply central limit theorem, but let’s apply it anyway. Suppose you know that the population variance, σ2 = 5.25. 代写统计学作业
a.Suppose,someone observes only one of these 4096 combinations as a sample: (15, 16,17, 18). That person is testing the null hypothesis H0 : µ = 14.5 at level of significance, α = 0.05, based on this observed set of four Calculate the p-value that the person will get, using central limit theorem.
b.Calculatethe p-value numerically by using the 4096 X¯ values (do not use CLT here).hint: think about the graph from assignment 1 [question 1(f)] and use the second definition of p-value from slide 20, week-7.
c.Why do you see a difference in your calculation in part(a) and part(b)? And under whatcondition you expect these two numbers to be similar?
Question 2 (5 points) 代写统计学作业
The goal of this question is to “see” the distribution of a likelihood ratio test statistic. In other words, we want to see, if H0 is really true, what will be the distribution of W where
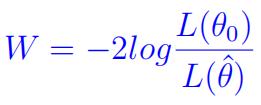
We will do this under two scenarios.
(a)SupposeX1, X2, …, X10 i∼id N (µ, σ2 = 9). Treat σ2 = 9 as the known constan We want to test H0 : µ = 5 vs H1 : µ ̸= 5 at level of significance, α.
(i)Write a function in Rthat
- generates 10 samples from a N (µ = 5, σ2= 9) distribution
- evaluatesthe likelihood function at µ = 5 (save it under the name L_theta0)
- evaluatesthe likelihood function at µ = x¯ (save it under the name L_theta1)
- calculates and returns −2 ∗log(L_theta0/L_theta1) 代写统计学作业
(ii)Runthis function using the replicate() command (or something similar) and save the output under the name LRT _vec.
(iii)Plot a density histogram usingLRT _vec.
code hint: use hist() with options freq=FALSE, breaks=50.
(iv)Overlaya χ2 density curve on top of this histogram.
code hint: generate 100000 random samples from a χ2 , use denisty() and lines()
(b)(we will repeat the process of part(a) but with a different distributionhere)
Suppose X1, X2, …, X10 i∼id P ois(λ).
We want to test H0 : λ = 5 vs H1 : λ ≠ 5 at level of significance, α.
(i)Write a function in Rthat
- generates 10 samples from a P ois(λ = 5)distribution
- evaluatesthe likelihood function at λ = 5 (save it under the name L_theta0)
- evaluatesthe likelihood function at λ = x¯ (save it under the name L_theta1)
- calculates and returns −2 ∗log(L_theta0/L_theta1)
(ii)Runthis function (100000 times) using the replicate() command (or something similar) and save the output under the name LRT _vec. 代写统计学作业
(iii)Plot a density histogram usingLRT _vec.
(iv)Overlaya χ2 density curve on top of this histogram.
(c)Inboth parts (a) and (b), your histograms should match(almost if not completely) with
density. Make a brief comment on what role you expect the sample size to play inthe closeness of the histograms and the density. (In other words, do you expect these type of closeness irrespective of the value of n?)
Question 3 (5 points) 代写统计学作业
In lecture-8 (day 2), we demonstrated the Newton-Raphson algorithm and Fisher’s scoring algorithm for solving score equations for Exponential distirbution. You will implement these two algorithms for the Bernoulli distribution.
Suppose this following observations are randomly drawn from Bernoulli(θ) distribution.
## 1 1 1 1 0 1 0 1 1 1
a)Byusing a random number between 0 and 1 as the initial guess, implement the N-R algorithm in R to find the MLE of θ. Use the following updating equation that we have learned in the class
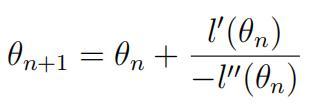
b.Changethe updating equation to the following (so called Fisher’s scoring method) and implement the algorithm to find the MLE of θ.
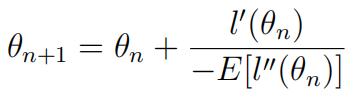
c.Try different value as your initial guess and compare the performances of the two updating (hint: one of them will sometime fail to give you the solution or will require more iterations to converge. Keep trying different initial values until you are able to see this difference).
Question-4 (1 point) 代写统计学作业
- Question1-3 are worth 14 points in
- Hereis a video on how to use R-markdown. https://play.library.utoronto.ca/watch/d b75830ca374b589e5453aeadf248ba2
- Thefinal 1-point of the assignment will be awarded if you use R-markdown to write your assignment (i.e. to write your answers to Ques 1-3).
