Lineare Algebra I
(Klausur zur Studienleistung)
代写线性代数 Bearbeitungszeit (digitale Abgabezeit inklusive): 120 Minuten. Erlaubte Hilfsmittel: Ein eigenhändig handschriftlich beschrifteter DIN A4
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –
- Bearbeitungszeit (digitale Abgabezeit inklusive): 120 Minuten.
- Erlaubte Hilfsmittel: Ein eigenhändig handschriftlich beschrifteter DIN A4
- Jeder Betrugsversuch hat den Ausschluss von der Klausur und das Nichtbestehen der Klausur zur Folge.
- Alle Lösungen sind zu begründen!
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –
Angaben des Prüflflings:
Name, Vorname:
Matrikelnummer:
Ich erkläre meine Prüfungsfähigkeit: ja / nein
– – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – – –
Erreichte Punktzahl:
Note:
Bremen, denAlle Aufgaben zusammen ergeben maximal 70 Punkte. Um zu bestehen brauchen Sie 40 Punkte

1.Zeigen Sie, dass B1 eine Basis von Q2 ist.
2.Geben Sie die Matrixdarstellung der linearen Abbildung T an, bezgl. derkanonischen Basen in Q2 und Q3 an.
3.Finden Sie den Kern von T.
4.Ermitteln Sie die Dimension von BildT.
5.Entscheiden Sie ob T injektiv und/oder surjektiv ist.
6.Geben Sie eine Basis von BildT an.
Aufgabe 2 (20 Punkte). Sei 代写线性代数
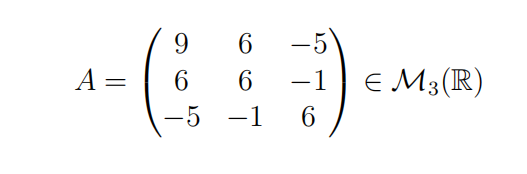
1.Entscheiden Sie, ob A invertierbar ist, und fifinden Sie A-1 ggf.
2.Ermitteln Sie den Rang von A sowie die Determinante.
3.Berechnen Sie A2 = A · A.
4.Untersuchen Sie die lineare Abhängigkeit der Spaltenvektoren von A.
Bitte umblättern!
Aufgabe 3 (15 Punkte). Sei, wie in voriger Aufgabe 代写线性代数

Aufgabe 4 (5 Punkte). 代写线性代数
Sei K ein Körper, V ein n-dimensionaler K Vektorraum. Seien U, W ≤ V Unterräume von V mit dim U = n − 1.
Zeigen Sie, dass dim(U ∩ W) ≥ dim(W) − 1.

更多代写:personal statement计算机代写 新加坡统计Final exam代考 英国econ代考价格 新加坡edu essay代写 Personal Statement个人陈述代写 东田纳西州立大学代写
