代写数学金融作业 MF 803代写

MF 803: Advanced Programming for Mathematical Finance

代写数学金融作业 Compute the daily residuals si,tin (1) for each sector ETF. What is their mean and variance? Do they appear to be normal?

Problem set # 2  代写数学金融作业

Due: Wednesday, September 25th, by 6:30pm.

1.SectorETF Factor Modeling: Consider again the following universe of ETFs:

Ticker   Description

SPY    S&P Index

XLB   Materials

XLE   Energy

XLF   Financials

XLI   Industrials

XLK   Technology

XLP    Consumer Staples

XLU     Utilities

XLV   Healthcare

XLY    Consumer Discretionary

(a)Download historical data on the Fama-French factors from Ken French’s website and write a piece of code that parses them into a Python dataframe (or other similar structure). Validate and clean data.

(b)Calculatethe daily covariance matrix of the factor returns over the entire time  Are the factors highly correlated? Compare these correlations to the correlations of the sector ETFs that you calculated in HW1. Are they more or less correlated?

(c)Calculate rolling 90 day correlations for the factor returns. Are they stableover time? Are they more stable than the correlations of the ETFs from HW1?

(d)Check the factor returns for normality using your favorite test. Do the factor returns appearnormal?

(e)Consider a multi-factor model for the sector ETFs using the Fama French returndata as variables. That is:

ri,t = β1rmkt,t + β2rsize,t + β3rbtm,t + si,t (1)

NOTE: This is the 3-factor Fama-French model. You may also choose to use a different set of Fama-French factors available on Ken French’s website.  代写数学金融作业

For each sector ETF, compute it’s β to the Fama-French factors using the above model. Compute the β for the entire historical period and also compute rolling 90-day β’s. Are these β’s more consistent than the single factor model β’s that you obtained in your first homework?

(f)Compute the daily residuals s_i,tin (1) for each sector ETF. What is their mean and variance? Do they appear to be normal? What does this tell you about the appro- priateness of the model? Can you think of any other tests of the residuals that would help you judge the model?

2. Exotic Option Pricing via Simulation  代写数学金融作业

Consider again a one-year ftxed strike lookback option which enables the buyer to choose the point of exercise for the option at its expiry. The Bachelier model can be written as:

dS_t = r dt + σ dW_t (2)

Assume that r = 0, S₀ = 100 and σ = 10.0.

(a)Generate a series of normally distributed random numbers and use these togenerate simulated paths for the underlying asset.  代写数学金融作业

(b)Plot a histogram of the ending values of the asset price along the simulated paths. Arethe ending values of your simulated paths normally distributed? Check using your favorite normality  test.

(c)Calculate a simulation approximation to the price of a Lookback put option with strike100 under the Bachelier  Compare the price of the lookback option in the Bachelier model to the Black-Scholes model price obtained in HW1.

(d)Calculatethe delta of the lookback option using finite differences as discussed in  That is:

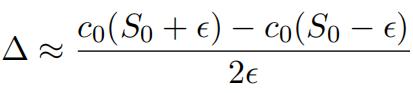
(3)

Try for several values of s and plot the calculated ∆ against the choice of s. Comment on what you think is the optimal value of s and what values lead to the largest amounts of error.

NOTE: All code for completing these exercises should be completed either in Python or C++ and should be written generically. You may end up using this code on future assignments so I encourage you to code thoughtfully.

 

更多代写：统计学网课代上  gre代考价格  金融网课代上  美国Online exam代考价格  美国Research Proposal代写  Eassay plan怎么写

合作平台：essay代写 论文代写 写手招聘 英国留学生代写