Computational Methods Summer 2022
HOMEWORK 1
代写数值分析 Usingthe Bisection Method with an error tolerance of 10−8, solve for x and then use this to find the roughness factor φ.
Homework should be handed in individually, though you may work with others and col- laboration is encouraged. Some of the problems should be solved using MATLAB. When using MATLAB, please follow the guidelines specified in ELMS (in particular see the file “Formatting MATLAB assignments”).
Dependence of problems on lectures:
Problem 1, Lecture (00), Bisection Method, May 31 代写数值分析
Problem 2, Lecture (01), FPI, June 1
Problem 3, Lecture (02), Newton’s Method, June 2

1.Inthe study of turbulent fluids, the so-called roughness factor φ satisfies the nonlinear equation 代写数值分析
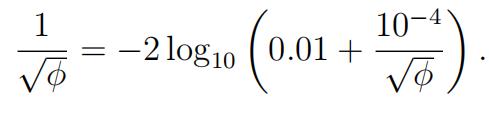
(a)Makethe substitution x = 1/√φ in the equation, and plot the two functions in a single Use this to explain why a solution exists in the interval 0 < x < 4, and that the solution is unique. (You should also know how to prove this interval contains a solution using the Intermediate Value Theorem.) 代写数值分析
(b)Usingthe Bisection Method with an error tolerance of 10−8, solve for x and then use this to find the roughness factor φ. Modify your code to keep track of the relative errors E(n) = xn+1 xn / xn , where xn denotes the approximate solu- tion at the nth iteration (n = 1, 2, 3, …). Plot the errors (i.e. plot the collection of points (n, E(n)), using a semilogarithmic y-axis. The MATLAB command for this is semilogy. You may modify m for this problem.
2.Considerthe equation x3 − x + ex = 0. 代写数值分析
(a)Plot the function to obtain a rough guess of the solution.
(b)Rewrite the equation as a fixed point problem x =g(x), for some function g.
(c)Write a script in MATLAB to carry out 10 steps of fixed point iteration (use a for loop to do this). Starting with your approximate solution from part (a), run your script to obtain the solution accurate to 6 decimal places. [If your iteration fails, your function g is probably not a contraction map near the Go back to part (b) and rewrite it as a different fixed point problem. Then try the iteration again with your new g.] 代写数值分析
3.(a)Write down Newton’s method to solve f (x) = 0 where f (x) = x1/3, and sim- plify the right-hand Use this to explain why Newton’s method fails to find the root x = 0 if starting from any x0 0.
(b) Can Newton’s method be used to find a solution of f (x) = 0 where f (x) =x 3, starting with x0 = 4? Explain. Would it work if we start at any point 3 < x0 < 4?

