ECO 5116 – PhD Micro II
Problem Set # 1
代写微观经济作业 Argue that (pure) strategy M is never a best response for player 1 to any independent randomizations by players 2 and 3.
1 Strictly Dominant Strategies 代写微观经济作业
(a) Prove that (i) there can be at most one strictly dominant strategy for any player in a fifinite game, and (ii) that any such strategy must then be a pure strategy.
(b) Prove that in the defifinition of a dominant strategy, it is suffiffifficient to check against “pure strategy” conjectures, (i.e., for all s−i ∈ S−i) rather than all conjectures (µi ∈ Σ−i). In other words, show that
ui(si , s−i) > ui(s 0i , s−i) ∀ s 0i ∈ Si , ∀ s−i ∈ S−i
implies
ui(si , µi) > ui(s 0i , µi) ∀ s 0i ∈ Si , ∀ µi ∈ Σ−i
2 IEDS
For each of the following games,
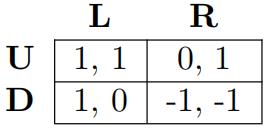
(i) which strategies survive the iterated elimination of dominated strategies (IEDS)?
(ii) which strategies are rationalizable for each player?
(iii) identify a Nash Equilibrium for each game (at least one).
(a.)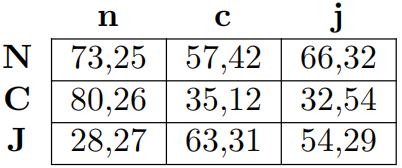
(b.)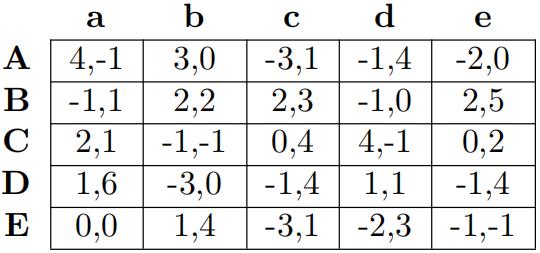
(c.)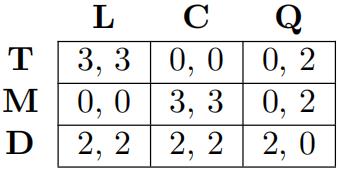

3 Independent vs. Correlated Rationalizability
This question is MWG Exercise 8.C.4, which has a typo in the bottom left cell of the table(the fifirst η should be π). So, use the corrected table below.
Consider a game ΓN with players 1, 2, and 3 in which S1 = {L, M, R}, S2 = {U, D}, and S3 = {l, r}. Player 1’s payoffffs from each of his three strategies, conditional on the strategy choices of players 2 and 3 are depicted as (uL, uM, uR) in each of the four boxes shown below,where π, ε, η > 0. Assume that η < 4ε. 代写微观经济作业
Note that this is not a payoffff matrix in the usual way – the three numbers are all payoffffs for player 1; payoffffs for players 2 and 3 are not shown.

(a) Argue that (pure) strategy M is never a best response for player 1 to any independent randomizations by players 2 and 3. (Luke edit: i.e., conjectures that disallow correlation in player 1’s conjecture about player 2’s and player 3’s strategies.)
(b) Show that (pure) strategy M is not strictly dominated.
(c) Show that (pure) strategy M can be a best response if we allow for player 1’s to hold “cor-related” conjectures – i.e., if 1’s conjectures about player 2’s and player 3’s randomizations can be correlated.
4 Finding Nash Equilibria 代写微观经济作业
This is partly from Jehle & Reny, Exercise 7.10. Answer each of the following:
(a) Find all Nash equilibria of the following game:
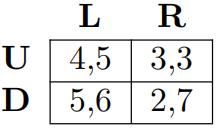
(b) Find all Nash equilibria of the following game:
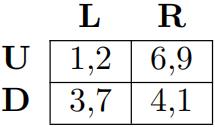
(c) Show that in the following game, there are two Nash equilibria, but only one in which neither player plays a weakly dominated strategy. 代写微观经济作业
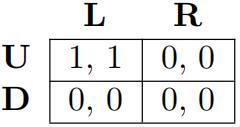
(d) Show that for the following game, there are infifinitely many Nash equilibria (and describe them), but only one in which neither player plays a weakly dominated strategy.