代写多变量微积分作业 MATH2720代写 Calculus代写

MATH2720 Multi-variable Calculus: Assignment 4

代写多变量微积分作业 You must submit your signed Academic Integrity Declaration form and completed problem set on Crowdmark by the deadline.

CrowdMark Instruction

We will be using Crowdmark to grade assignment/test submissions. You will get a personalized submission link sent to your UManitoba email address. Do NOT share this link with other students.

If you cannot find the notification email in your inbox, check your spam folder or search your email for all emails containing the word ”crowdmark.”

If you really cannot find your link, contact Dr. Xinli (xinli.wang@umanitoba.ca) at least a day before the assignment deadline, and I will re-send it to you. Make sure you use the email policy so your email is not filtered out.

How do I write my solutions?  代写多变量微积分作业

• Option 1: Write your answers electronically. Convert your solutions to pdf when you are done, such that each question starts in a new file.
• Option 2: Write your answers by hand. Then take a picture with your phone (not recommended) or scan your answers (using the library scanners, or a mobile app like Scanbot or Microsoft Office Lens or Google Drive (Android only)(recommended). Make sure each question starts in a new file, and that your picture/scan is clear and legible. You will receive no credit if your answers cannot be clearly read.

How do I submit my work?  代写多变量微积分作业

• Click the link in your notification email from Crowdmark.
• Upload your answers to each question separately. (You may use multiple pages perquestion)
• Rotatepages if necessary, and order pages correctly for each question.
• Submit.
• Save a copy of the confirmation page for your records.
• You are allowed to change your answers by resubmitting as many times as you need before the deadline.

Submission of Assignment

You must submit your signed Academic Integrity Declaration form and completed problem set on Crowdmark by the deadline.

• Late assignments will not be accepted.
• Consider submitting your assignment well before the deadline.
• If you require additional space, please insert extra pages.
• You must justify and support your solution to each question.

Academic Integrity Declaration  代写多变量微积分作业

Declaration: I, the undersigned, declare that all the work I will submit to fulfill the requirements for this assessment  is wholly my own work. During the test/exam I will not:

1. copy by manual or electronic means from any work produced by any other person or persons, present or past, including tutors or tutoringservices;
2. share questions or answers in whole or in part with anyone, including posting portions of the test/exam in publicly accessiblelocations;
3. copy from any source including textbooks and websites,or
4. consultexternal websites, online forums, search engines,  or any resource not appearing in the list of acceptable test materials above.  代写多变量微积分作业

Students must not discuss or communicate the contents of the test or exam with any person except their instructor until 24 hours after the end of the test or exam.

By signing this document, I acknowledge that I have read and will follow the instructions for acceptable material during the test/exam.

I understand that penalties for submitting work which is not wholly my own, or distributing my work to other students, isconsidered an act of Academic Dishonesty and is subject to penalty as described by the University of Manitoba’s Student Discipline Bylaw. These penalties that may apply range from a grade of zero for work, failure in the course, to expulsion from the University.

Name:                                      

 

Student number:                                            

 

Date:                                                 

 

Signature:                                          

List of problems  代写多变量微积分作业

D\L	−80	−70	−60	−50	−40	−30	−20	−10	0	10	20	30	40	50	60	70	80
1	1440	1440	1122	977	897	843	799	762	727	693	657	615	563	489	362	0	0
32	1440	1225	995	904	850	811	779	753	727	702	676	646	610	559	478	292	0
60	1183	914	841	804	780	763	749	737	727	715	705	692	677	656	626	567	378
91	551	640	671	687	699	707	714	720	726	733	740	748	759	773	796	839	975
121	208	549	514	582	625	656	682	706	727	749	772	799	833	881	958	1131	1440
152	0	0	383	502	571	621	660	695	727	760	796	836	888	964	1097	1440	1440
172	0	0	352	484	559	613	655	698	727	763	801	845	901	982	1132	1440	1440
182	0	0	360	488	562	614	654	693	727	762	799	843	898	978	1123	1440	1440
213	0	253	461	549	603	641	673	701	727	753	782	815	856	915	1013	1281	1440
244	333	550	616	649	672	689	702	715	726	738	752	766	785	811	851	932	1252
274	904	808	777	760	750	742	736	731	726	722	718	713	707	701	690	671	616
305	1440	1107	947	874	828	796	770	758	727	707	685	660	630	589	524	390	0
335	1440	1440	1091	960	887	836	794	760	728	695	661	622	573	505	389	0	0
356	1440	1440	1133	983	901	845	801	763	728	693	655	613	559	485	353	0	0

Table 1: Number of minutes of sunlight.

1.Table 1 shows M (D, L), the number of minutes of sunlight per day as a function of the day D of the year and latitude L.  代写多变量微积分作业

Positive latitudes indicate degrees north of the equator, negative latitudes indicate degrees south of the equator. (Note: Grand Rapids is at approximately 43^◦ latitude.)

(a)Estimate as best you can each of the first order partial derivatives and write one sentence that describes,  in context, the meaning of the derivative. Include appropriate units in your description.

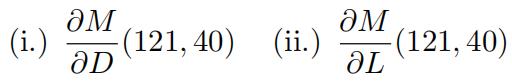
(b)Estimate as best you can each of the second order partial derivatives and write one sentence thatdescribes, in context, the meaning of each. Include appropriate units in your description. Carry your approximations to two decimal places. Is Clairaut’s Theorem satisfied? Explain.  代写多变量微积分作业

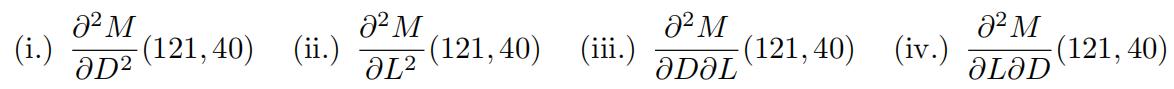
2.Findthe limit, if it exists, or demonstrate that the limit does not exist.

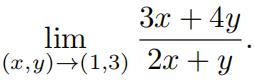
(a)

(b)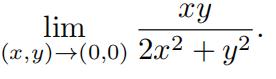

3.Find all first and second order partial derivatives.

(a)f(x, y) = y² − cos(xy)

(b)

 

更多代写：多伦多代写  GRE代考  工商代写  批判性散文代写  人力资源代写论文  pte代考靠谱吗

合作平台：essay代写 论文代写 写手招聘 英国留学生代写