ECON0027 Game Theory
Home assignment 5
代写博弈论 There are N potential contractors to choose from. Each contractor is characterized by a cost ci of building the bridge.
1.Four students are choosing colleges to go to. 代写博弈论
There are four colleges and each college can accept only one student. Students’ preferences are represented by the following lists:
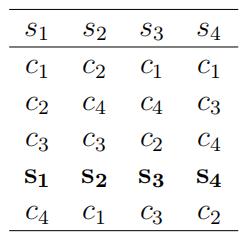
Each college has preferences (rankings) over students which is represented by the following lists:
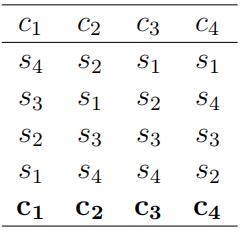
(a) Suppose the allocation of student to schools is implemented using serial dicta- torship mechanism with the following ranking of students: s1, s2, s3, s4. Find this allocation.
(b) Suppose the students are initially allocated the seats in the following way: (s1, c4),(s2, c1),(s3, c3) and (s4, c2), and after initial allocation the government runs the top trading cycle mechanism where only students’ preferences are taken into account. Find the fifinal allocation of students to colleges generated by the mechanism. 代写博弈论
(c) Find a stable students-optimal allocation by running deferred acceptance al gorithm.

2.Consider a cooperative game in characteristic form with three players.
The value of a grand coalition is v({1, 2, 3}) = 10. The value of smaller coalitions are v({1, 2}) =v({1, 3}) = v({2, 3}) = z, where z is a parameter. Finally v({1}) = v({2}) =v({3}) = 1.
(a) Suppose z = 3. Find the core of this game.
(b) What happens to the core of the game when z gets larger.
(c) Find values of z for which the core of the game is empty.
3.Consider a world with k men and h women. 代写博弈论
Man i’s height is xi and woman j’s height is yj for all i and j. Assume that no two individuals in this world have the same height. Also assume that both men and women prefer taller partners to shorter ones. Finally, both men and women prefer to be married to being single.
(a) How many stable matchings are possible in this world? Find them.
(b) Are there any unstable Pareto effiffifficient matchings? Explain your answer.
(c) Suppose all women prefer shorter partners to taller ones. Is there more than one stable matching in this case?
4.Consider the government that wants to hire a contractor to build a bridge.
There are N potential contractors to choose from. Each contractor is characterized by a cost ci of building the bridge. The cost is drawn independently from a uniform distribution with the support [α, β], where β > α > 0. Each potential contractor knows its own cost, but does not know the costs of others. All contractors are risk-neutral expected profifit maximizers.
(a) Suppose a government decides to run a second-price sealed bid tender to select a contractor. All potential contractors simultaneously and independently submit their quotes to the auctioneer. A contractor who submits the lowest quote, gets the contract. The government pays this contractor the second lowest quote. This tender is similar to the second-price sealed bid auction, but since the government tries to minimize the expenditure, it selects the lowest price, rather then the highest price. Argue that submitting contractor i’s own private cost ci as a quote is a weakly dominant strategy for contractor i. 代写博弈论
(b) Suppose a government decides to run a fifirst-price sealed bid tender to select a contractor.
All potential contractors simultaneously and independently submit their quotes to the auctioneer. A contractor who submits the lowest quote, gets the contract. The government pays this contractor his quote. This tender is similar to the fifirst-price sealed bid auction, but since the government tries to minimize the expenditure, it selects the lowest price, rather then the highest price. Write down the payoffff maximization problem for a contractor i. What is the expected probability of winning the tender for a contractor i if he submits a quote bi .
(c) Find a symmetric Bayesian Nash Equilibrium in the fifirst-price sealed bid tender described above. You can assume that in this equilibrium a contractor with the highest type possible submits a quote that is equal to his costs: ci = β =⇒ bi = β (Hint: it may be useful to make the following change of variables:
![]() and
and![]() . If you do so, give the intuition about what these new variables represent.)
. If you do so, give the intuition about what these new variables represent.)

