Computer Vision
Assignment

Please type your solutions to Problems 1 and 6 using a word processor(Word or Latex.). For Program use Matlab, submit as hard copy a short (100-200 word) report in Word or Latex. In this report briefly explain the features of your program, any findings and conclusions. Provide outputs (images) to support your report. Each image must have a detailed caption explaining what processing has been done, etc.
This assignment carries 110 points, plus 15 points extra credit for exceptionally well done work.
1. (a) [6 points] Let f(x,y) be an image. Let h(x,y) be the image obtained by applying the a 3 by 3 spatial low pass mask (averaging filter) to f(x,y). Similarly let g(x,y) be the image obtained by applying a 3 by 3 spatial high pass mask to f(x,y). Prove that
g(x,y) = f(x,y) – h(x,y)
Note: one or more examples do not constitute a proof.
(b) [5 points] Is the high pass mask separable? What is the implication of separability on computations?
2. [4+5 points] Suppose that the image gray level values under a mask are
3 2 1
7 8 4
3 6 5
Determine the value of the corresponding pixel in the output image for:
(a) Median, (b) Harmonic mean.
In each case comment on the suitability of the filter for reducing Gaussian noise, and provide reasoning for your comments.
3. [8 points] Find the output images if Sobel edge operators are applied to the following 8 by 8 input image. Note that you will have three gradient images, one in x-direction, one in y-direction and one gradient magnitude. Ignore the border effects, and produce only 6 by 6 output images.
2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 7
2 2 2 2 2 2 7 7
2 2 2 2 2 7 7 7
2 2 2 2 7 7 7 7
2 2 2 7 7 7 7 7
2 2 7 7 7 7 7 7
2 7 7 7 7 7 7 7
4. (a) [6 points] Use the definitions of the derivatives as 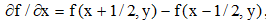 , and similarly for
, and similarly for 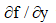 to obtain the Laplacian mask. Why is Laplacian is rarely used alone.
to obtain the Laplacian mask. Why is Laplacian is rarely used alone.
(b) [4 points] What will be the Laplacian mask if the derivative is defined as 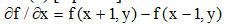 , and similarly for
, and similarly for 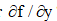 ? Why is this definition is not suitable for obtaining the Laplacian?
? Why is this definition is not suitable for obtaining the Laplacian?
5. [7 points] Compute the Fourier transform of the one-dimensional image f(0) = 8, f(1) = 4, f(2) = 2, f(3) = 1. Find Fourier spectrum |F(u)|. Comment on your results.
6. [4+4+4+4 points] Answer the following questions and support your answers with reasoning and analysis
(a) Why is it necessary to move the origin of the Fourier transformed image to the
center (i.e. to u = n/2, v = n/2). How is this shifting implemented?
(b) Why is bit reversal needed in FFT? Explain.
(c) The Fourier spectrum |F(u,v)| of an image f(x,y) is known, but f(x,y) is not known.
Can f(x,y) be computed? Explain.
(d) Prove that the two-dimensional Fourier transform of an image f(x,y) can be
achieved using two one-dimensional transforms. What is the significance of this?
Programming [30+20 points]
A. The purpose of this programming assignment is to explore and then propose a good edge detection method for color images. Use the images posted to demonstrate your results There are a number of ways to perform edge detection, for example:
(i) Convert the image into greyscale and find the edges using the Sobel method (gradient in x and y directions and the magnitude),
(ii) Perform edge detection for each color component separately, then combine the three edge images somehow (e.g. find gradient magnitude of each color and add and average them, or find gradients of each color in x and y then find the gradient magnitude),
(iii) Treat each pixel color as a vector say V(x,y) in (RGB) space and find the vector differences V(x+1,y)-V(x-1,y) and V(x,y+1)-V(x,y-1) and then the magnitude.
In your report explain what method you used and why, and possible comparisons between the various methods (i.e. the above 3 and your own).
B. Now add salt and pepper noise to the image by randomly selecting 20% of the pixels and setting the selected pixel randomly to either back or white. Show the results of edge detection without filtering noise and with filtering noise using an appropriate filter.
For each part A and B, write a short report about any special feature of your program and your findings, make comments and conclusions. If you wish, you can experiment with different percentages of noise affecting pixels,
