Assignment 13: Actuarial Present Value
代写会计作业 The probability of survival is highest in the early years of the annuity, and declines each year (recall the Gompertz mortality equation).
Background
- The Gompertz Equation models an individual’s probability of survival to a certain age.
- The expected value provides the probability-weighted financial payout of an uncertain event.
- The present value is the discounted amount that corresponds to a known future value.
- The actuarial present value (APV) combines these ingredients to find the expected present value of future amounts that depends on an individual’s survival.
Part A: Pricing Annuities 代写会计作业
A lifetime annuity is a stream of payments that continues for the rest of the owner’s life.Insurance companies sell annuities and guarantee to make the payments each month. For example, a 65-year old might buy an annuity contract that promises to pay $1,000 per month ($12,000 per year) for the rest of his life. In this assignment, you will build a calculator to find the value (i.e., fair price) of an annuity.
There is uncertainty about whether the purchaser of the annuity will survive to collect each payment. The probability of survival is highest in the early years of the annuity, and declines each year (recall the Gompertz mortality equation).
Begin with the spreadsheet (called pricing-annuities.xls) that is available on blackboard.
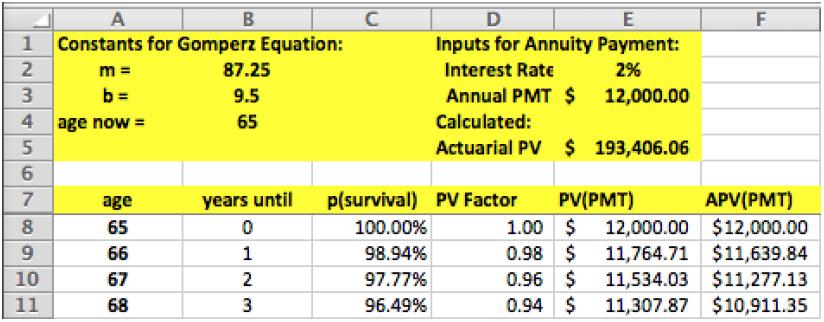
Note that the survival probability (i.e., using the Gompertz equation) is already implemented in column C. The survival probability for each year in the table depends on the inputs in cells B2, B3, and B4.
- To begin, extend the table to allow for account for up to 80 years of annual payments.
- In column D, calculate the present value factor, i.e., 𝑃𝑉𝐹 =
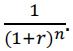
- In column E, calculate the present value of each year’s payment, i.e., 𝑃𝑉 = 𝑃𝑀𝑇 × 𝑃𝑉𝐹.Assignment 13: Actuarial Present Value
- In column F, calculate the APV for each year. The APV is the present value of the payment multiplied by the survival probability for that age.
- Notice that cell E5 will calculate the sum of the actuarial present value for all years. This is the “fair” price of the annuity.

Part B: Questions to Answer 代写会计作业
For each question/part, make a copy of the spreadsheet to a new tab. For simplicity, you may assume annual payments at the rate of 12 times the monthly payment amount.
- Use the population parameters of m = 85 and b = 9.5. Consider Maria who is 65 years old. The Great Big Insurance Company offers to sell Maria an immediate lifetime annuity for $200,000, which will pay her $1,400 per month for the rest of her life.Assume an interest rate of 5%.
- What is the fair value for this annuity?
- What would be the fair value of this annuity if Maria were 67 years old today?
- What would be the fair value of the annuity if Maria were 65, but the interest rate was only 4%?
- In the United States, qualified retirees receive Social Security retirement benefits, which are effectively and inflation-adjusted lifetime annuity. Benefits are paid in real dollars at an amount set based on the pre-retirement income and the age at which the retiree begins to receive benefits. 代写会计作业
Consider Hasan, who is currently age 62 and considering when to begin receiving benefits. Use your annuity calculator, with population parameters of m = 90, b = 9.5, and a real interest rate of 1% per year. Find the actuarial present value for each of the options (a, b, c) below.
He has to decide between three options from which to choose:
- Receive $1,279 per month, for the rest of his life, starting at age 62.
- Receive $1,856 per month, for the rest of his life, starting at age 67.
- Receive $2,332 per month, for the rest of his life, starting at age 70.
Which option you would recommend to Hasan? Write a brief explanation, and use the actuarial present value to make your case.
What to Submit
Submit your Excel spreadsheets with all calculations and answers to the questions.

更多代写:澳大利亚加拿大代考 gre保分 会计学网课代做 加拿大经济学Essay代写 加拿大论文代写范文 公司法和商业法代考
