Winter Examination Period 2023 — January — Semester A
代写人工智能final Calculators are permitted in this examination. Please state on your answer book the name and type of machine used.
ECS759P ARTIFICIAL INTELLIGENCE
Duration: 2 hours
This is a 2-hour online exam, to be completed during a fifixed 4-hour window.
You MUST submit your answers before the exam end time.
All instructions and guidelines from the exam page should be followed.
This is an open-book exam and you may refer to lecture material, text books and online resources. The usual referencing and plagiarism rules apply, and you must clearly cite any reference used.
Calculators are permitted in this examination. Please state on your answer book the name and type of machine used.
Answer ALL questions 代写人工智能final
You MUST adhere to the word limits, where specifified in the questions. Failure to do so will lead to those answers not being marked.
YOU MUST COMPLETE THE EXAM ON YOUR OWN, WITHOUT CONSULTING OTHERS.
Question 1
A milkman has a full bottle containing 25 litres of milk and two empty bottles with capacities of 17 litres and 7 litres respectively. He needs to deliver exactly 1 litres to a customer in one of these bottles without wasting any milk. That is, he can only pour milk between the bottles, and he has no means of measuring except knowing when a bottle is full.
(a) Formulate this problem as a search problem by specifying how you would represent:
(i) a general state,
(ii) the initial state,
(iii) the operators (actions that can be performed, and how the new state is computed),
(iv) the goal test,
(v) the path cost.[10 marks]
(b) Estimate the size of the search space (i.e. the number of all possible states) and the maximum branching factor, explaining your reasoning.[4 marks]
(c) What are the fifirst 3 nodes expanded in searching for a solution using breadth-fifirst search? Show the initial agenda and the resulting agenda after each node expansion.[7 marks]
(d) Would uniform cost search be better than breadth-fifirst search for this problem? Give a reason for your answer.[2 marks]
(e) Why is depth-fifirst search not suitable for this problem? How can depth-fifirst search be modifified to make it suitable for this problem?[2 marks]
Question 2 代写人工智能final
(a) Consider the 4-queen puzzle problem: We have a 4×4 board and 4 (chess) queens.
We would like to place the queens on the board so that no two queens threaten
(attack) each other. Recall that queens threaten each other row-wise, column-wise,
and diagonally (all the possible diagonals are considered)!
Suppose the initial arrangement of the queens is as follows:
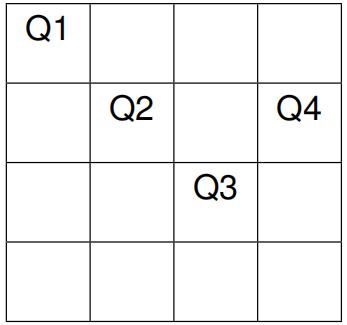
We represent a state (an arrangement of the queens on the board) with the tuple (i1, i2, i3, i4) where i1, i2, i3, i4 represent the row of the queen in the fifirst column (Q1), second column (Q2), third column (Q3), and the forth column (Q4), respectively. So the initial state in the fifigure will be the tuple of (1, 2, 3, 2), since Q1 is in the fifirst row,Q2 in the second row, Q3 in the third row, and Q4 in the second row.
Suppose we use the following heuristic function as the cost of each state: the total number of queen pairs that threaten each other. For instance, the cost associated with the initial state in the fifigure is 5, because the following pairs are threatening each other: {Q1, Q2}, {Q1, Q3}, {Q2, Q3}, {Q2, Q4}, {Q3, Q4}.
Execute two search steps of the Hill-Climbing algorithm for this problem, starting from the given initial state. In each search step, specify
(i) The current state and the current cost;
(ii) Neighbouring states and their costs;
(iii) The best neighbouring state.
Notes:
- Recall that a notion of a neighbouring state is one that we can change to by moving one queen to any position within its own column in one move. For instance, (4, 2, 3, 2) is a neighbour of the above initial state (moving Q1 to the last row), but (2, 2, 1, 2) is not (since it involves moving both Q1 and Q3).
- If encountered with a tie-breaking situation (i.e. two or more neighbouring states with the same lowest cost), break the tie by applying the two following rules in order:
Rule 1: Favour moving the queen with the smallest index (i.e., the leftmost queen among the ties) if the ties are in different columns. 代写人工智能final
Rule 2: Favour moving the queen downwards (i.e., to the row with the highest index among the ties) if the ties are in the same column.[14 marks]
(b) In part (a), you will fifind that the search gets stuck at a local minimum after two search steps. Name and brieflfly describe two approaches aimed at solving the problem of being stuck at local minima.[4 marks]
(c) Explain in your words the purpose and use of the “temperature” variable in simulated annealing.[4 marks]
(d) In genetic algorithms, there are two search operators: crossover and mutation. Given that crossover can be used to explore the search space, explain why we need mutation.[3 marks]

Question 3
(a) Provide the two conditions that need to be true for solution x(1) to dominate solution x(2) in a multi-objective optimisation problem.
Given the plot below and considering that both objectives (f1 and f2) are minimisation objectives, provide the result of the dominance check for the two following pairs of solutions: A and C, A and B.[3 marks]
(b) Use a truth table to show that: P → (Q ^ ¬Q) ≡ ¬P [4 marks]
(c) Convert the following statements into First Order Logic (FOL):
(i) Everyone hates someone.
(ii) Someone hates everyone.
(iii) If any two people are friends to each other, then they are not enemies to each other. 代写人工智能final
(iv) Any two people are either friends to each other or enemies to each other.
(v) Everyone who Mary loves loves someone who is happy.[5 marks]
(d) Convert the four logical sentences below into conjunctive normal form, showing all work. Report all the steps (state “nothing to do” for the steps where this is the case).
- Allergy(x) → Sneeze(x)
- (Cat(y) ^ Allergic(x)) → Allergy(x)
- Cat(Tom)
- Allergic(Amy)
Negate and bring into conjunctive normal form the goal:
- Sneeze(Amy).
Give a resolution proof of this goal, showing and explaining your work.[7 marks]
(e) Compute the Crowding distance according to the NSGA-II algorithm for the three solutions in a multi-objective optimisation problem specifified in the table below. Values of the two minimisation objectives (f1 and f2) are provided for each solution. Maximum and minimum values per objective are given as follows: f1 min = 10, f1 max = 100,f2 min = 0.25, f2 max = 0.80. Show all work. Indicate one solution that will be chosen by the algorithm as least crowded.
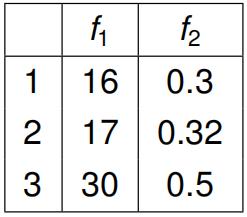
[6 marks]
Question 4 代写人工智能final
(a) Draw a diagram of a basic perceptron, and give the equation(s) relating its inputs,parameters and outputs. Explain how the step activation function is computed.[6 marks]
(b) Explain in detail how the backpropagation algorithm computes the following given a training example: (i) observed error; (ii) partial derivatives with respect to the output layer weights; (iii) partial derivatives with respect to the hidden layer weights.
Formulas can be expressed with words.
[4 marks]
(c) Given a single perceptron with inputs xi for 1 i < 3, where x3 = 1 is the bias, initial weights w1 = w2 = w3 = 1, learning rate ↵ = 0.5 and the following activation function:
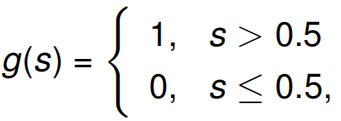
use the perceptron training algorithm to learn the function specifified by the following table of training examples. Show all work, including input (training example and the bias), weights, predicted output (after applying the activation function) and action performed for each step. Explain why the training stops.
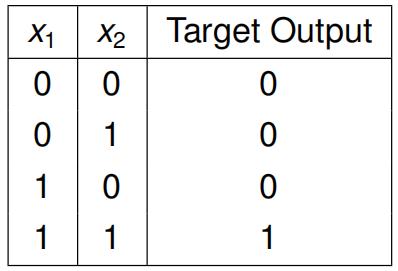
[8 marks]
(d) You are given a multiclass perceptron model which consists of the three single-layer perceptrons (A, B and C) with the respective sets of weights A, B and C provided as follows: wA = (1, 0, 0), wB = (0, 1, 0) and wC = (0, 0, 1). The perceptron that gives the maximum value in the output identififies the predicted class. For example, if perceptron
A predicts 1 and perceptrons B and C predict 0 then the predicted class is A. If there is a tie, A is chosen over B, B is chosen over C. Only the weights of two relevant perceptrons are updated at each step. For example, if the predicted class is A and the true class is C, then the input vector is added to the weights C and subtracted from the weights A. Learning rate is ↵ = 1 for all the perceptrons. The activation function is given as follows for all the three perceptrons:
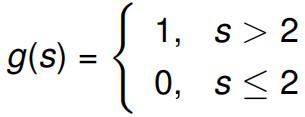
Provide the predicted class and updated weights after training once on each example from the training data as provided in the table below. Show all work.
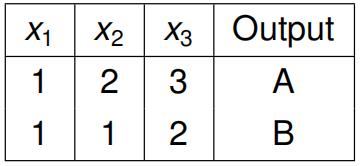
[7 marks]

