Assignment 3
代做统计学习作业 We can see that there are 4 equations and 4 unknown variables for each subintervals. Theerefore we can solve the systems of equations to generate
Question 1 代做统计学习作业
(a)
Take the derivative with regard to z, we have:
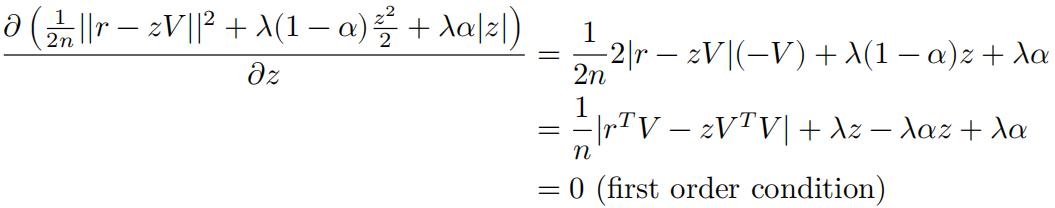
Now assume 𝑟T𝑉 − 𝑧𝑉T𝑉 > 0, then:
Completing the squares we have:
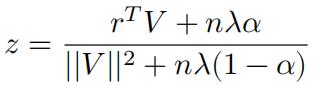
If 𝑟T 𝑉 − 𝑧𝑉T𝑉 < 0, we have:
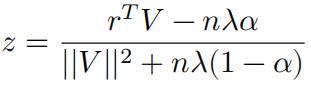
So the solution can be written with the soft-thresholding function:
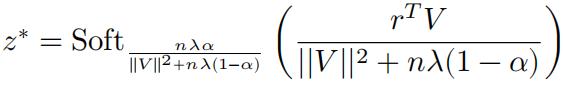
(b)
The coordinate descent algorithm is implemented below:
library(MASS)
set.seed(7)
n = 200
p = 20
V = matrix(0.2, p, p)
diag(V) = 1
X = as.matrix(mvrnorm(n, mu=rep(0,p), Sigma=V))
Y = X[,1] - 0.55 * X[,2] + 0.25 * X[,3] + rnorm(n)
X = scale(X)*sqrt(n/(n-1))
Y = scale(Y)*sqrt(n/(n-1))
1lambda=0.05
alpha=0.7
soft_thresholding = function(r,V,n,lambda=lambda,alpha=alpha){
LAMBDA= n * lambda * alpha / (sum(V*V) + n * lambda * (1-alpha))
XX = sum(r*V)/(sum(V*V) + n * lambda*(1-alpha))
one = (abs(XX)>=LAMBDA)+0
sign(XX)*(abs(XX)-LAMBDA)*one
}
P_coefficients = rep(0,p)
last_P_coefficients = rep(1,p)
while(sum(abs(last_P_coefficients - P_coefficients)) > 0.001){
last_P_coefficients = P_coefficients
for (i in 1:p) {
v=X[,i]
r = Y - X[,-i] %*% P_coefficients[-i]
P_coefficients[i] = soft_thresholding(r,v,n, lambda, alpha)
}
# print(sum(Y-X %*% P_coefficients))
}
cat("The coefficients solved by Coordinate Descent Algorithm\n")
## The coefficients solved by Coordinate Descent Algorithm
print(P_coefficients)
## [1] 0.588641037 -0.306612179 0.121252303 -0.009122607 0.000000000
## [6] 0.000000000 -0.009433374 0.000000000 0.038724823 0.000000000
## [11] -0.015128767 0.051720729 0.000000000 0.045485343 0.000000000
## [16] -0.035347828 0.000000000 0.000000000 0.089265079 0.000000000
library(glmnet)
## Matrix 代做统计学习作业
## Loaded glmnet 4.1-2
beta2 = glmnet(X,Y,alpha=alpha,lambda=lambda)
cat("The coefficients solved by Coordinate Descent Algorithm\n")
## The coefficients solved by Coordinate Descent Algorithm
print(beta2$beta)
## 20 x 1 sparse Matrix of class “dgCMatrix” ## s0
## V1 0.588641054
## V2 -0.306673740
## V3 0.121166808
## V4 -0.009175566 ## V5 .
## V6 .
## V7 -0.009466051 ## V8 .
## V9 0.038717671 ## V10 .
## V11 -0.015149746
## V12 0.051750157 ## V13 .
## V14 0.045517614 ## V15 .
## V16 -0.035304500 ## V17 .
## V18 .
## V19 0.089305834 ## V20 .
cat("Mean squared error\n")
## Mean squared error
print(1/p*sum((P_coefficients-beta2$beta)^2))[1] 1.045434e-09
Question 2
(a)
The ̃𝑔 exists because by the definition of natural cubic spline, we can define a cubic curve for each 
interval for i = 1 to n – 1. Inside each interval, thẽ𝑔 is a cubic function in the form of 
Then we can let̃𝑔(𝑥𝑖 ) = 𝑔(𝑥𝑖) for each i = 1 to n. And for the natural cubic spline to be smooth, we can also require the derivative of̃ 𝑔 ̃at each 𝑥𝑖 to be the same for two subintervals. We can see that there are 4 equations and 4 unknown variables for each subintervals. Theerefore we can solve the systems of equations to generate such a natural cubic spline.
(b) 代做统计学习作业
Following the hint, note that̃𝑔(𝑥) is linear at intervals (𝑎, 𝑥1 ) and (𝑥𝑛, 𝑏), therefore″ ̃𝑔(𝑥) = 0 for x = a, x= b; And that̃𝑔 is a natural cubic spline, so‴̃𝑔 (𝑥) is a constant for all 𝑎 = 𝑥 0 ≤ 𝑥 ≤ 𝑥𝑛+1= 𝑏.
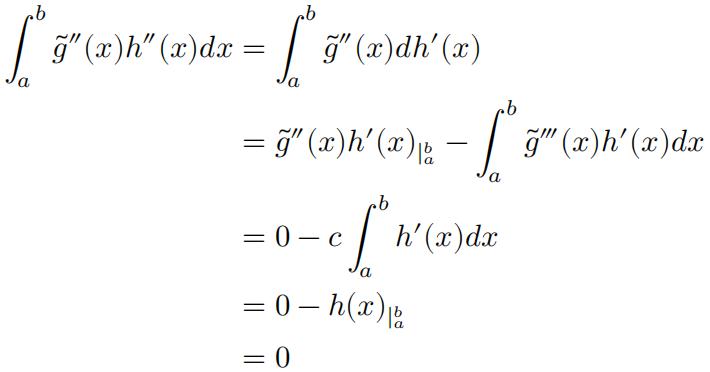
(c)
Note that 𝑔(𝑥) = ̃𝑔(𝑥) + ℎ(𝑥). So:
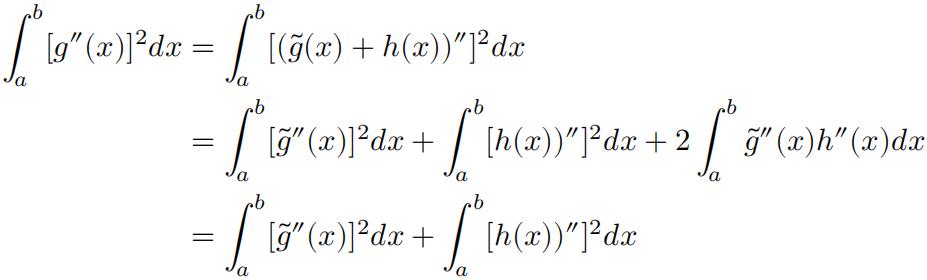
Question 3 代做统计学习作业
(a)
The 10-Fold cross validation is implemented as below.
library(MASS) library(splines) library(dplyr)
##
##
##
## ‘dplyr’
## The following object is masked from ‘package:MASS’: ##
## select
## The following objects are masked from ‘package:stats’: ##
## filter, lag
## The following objects are masked from ‘package:base’: ##
## intersect, setdiff, setequal, union
data("Boston")
all_dfs <- seq(1, 20)
cv_group = function(k, data_size){
set.seed(0)
cvlist = list()
n = rep(1:k, ceiling(data_size/k))[1:data_size]
temp = sample(n, data_size)
x = 1:k
dataseq = 1:data_size
cvlist = lapply(x, function(x) dataseq[temp==x])
return(cvlist)
}
cvlist = cv_group(10, nrow(Boston))
average_error = c()
for(df in all_dfs){
error = 0
for(i in 1:10){
train = Boston[-cvlist[[i]],]
test = Boston[cvlist[[i]],]
model = lm(nox~ns(dis, df=df), data=train)
prediction = predict(model, test)
# mean square error
error = error + sum((prediction - test$nox)^2)
}
average_error = c(average_error, error/nrow(Boston))
}
df = data.frame(df = all_dfs, mse = average_error)
plot(df$df, df$mse, type="l")
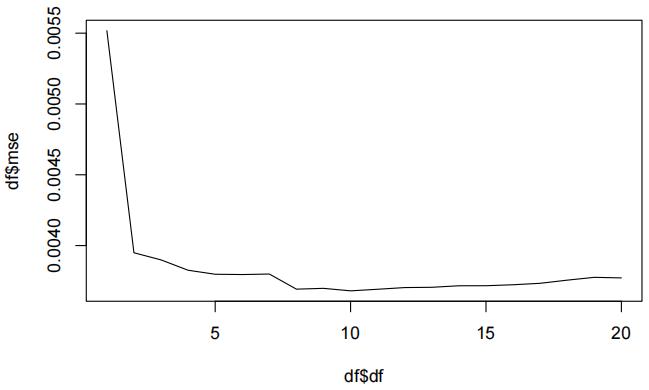
df
## df mse
## 1 1 0.005517658
## 2 2 0.003949362
## 3 3 0.003899021
## 4 4 0.003825912
## 5 5 0.003797626
## 6 6 0.003795578
## 7 7 0.003799139
## 8 8 0.003692330
## 9 9 0.003698045
## 10 10 0.003680476
## 11 11 0.003691626
## 12 12 0.003703575
## 13 13 0.003705500
## 14 14 0.003716244
## 15 15 0.003716586
## 16 16 0.003723415
## 17 17 0.003733690
## 18 18 0.003756013
## 19 19 0.003775849
## 20 20 0.003771833
We can see that with K = 10, the MSE is lowest. Now we will fit the model again with K = 10 and plot its fit.
library(ggplot2) model.best = lm(nox~ns(dis, df=10), data=Boston) predictions = predict(model.best, Boston) Boston$prediction = predictions ggplot(Boston) + geom_line(aes(x=dis, y=nox, color="NOX")) + geom_line(aes(x=dis, y=prediction, color="Predicted")) + labs(title="Boston Housing NOX Prediction")
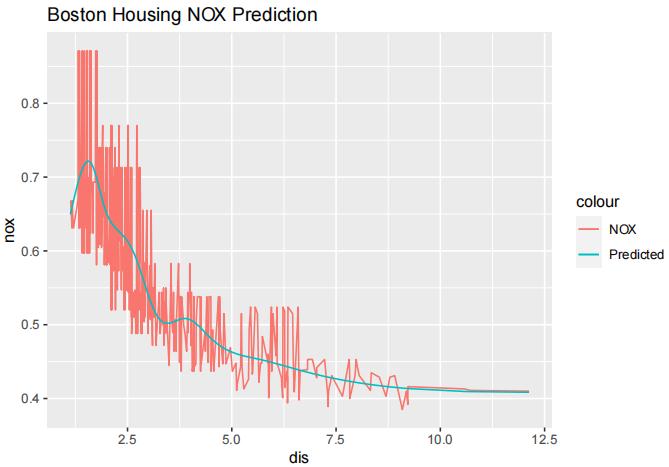
(b)
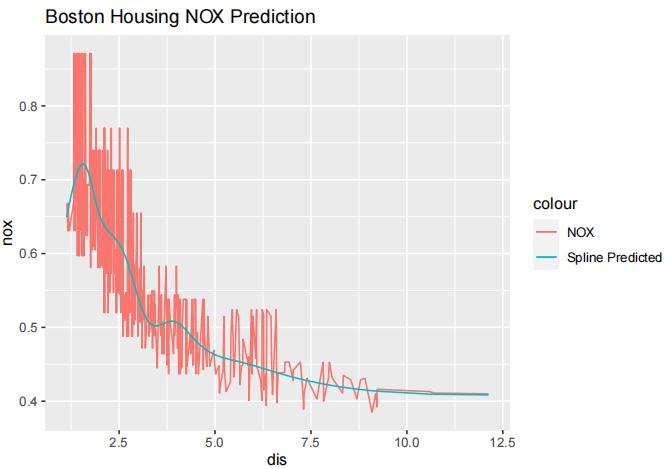
Using smooth.spline() to fit nox using dis:
model.spline = smooth.spline(Boston$dis, Boston$nox, cv=FALSE) predictions2 = predict(model.spline, Boston) Boston$prediction2 = predictions ggplot(Boston) + geom_line(aes(x=dis, y=nox, color="NOX")) + geom_line(aes(x=dis, y=prediction2, color="Spline Predicted")) + labs(title="Boston Housing NOX Prediction")
