MACM 201 – D100 AND D200 ASSIGNMENT #6
代做北美数学作业 Answer all questions on paper or a tablet using your own handwriting. Put your name, student ID number and page number at the top of each page.
Instructions
Answer all questions on paper or a tablet using your own handwriting. Put your name, student ID number and page number at the top of each page. If you use paper make a photo of each page and upload your solutions to crowdmark. If you use a tablet, export your assignment to .pdf and upload the .pdf to crowdmark.
Textbook Reading
- Sections: 10.4, 9.5, 11.1, 11.3
Defifinitions, Concepts & Keywords:
- Be able to solve linear recurrences using generating functions.
- Be able to use proof by induction to prove summation formulas.
- Know what a multi-graph, walk, Euler circuit, and Euler trail is.
- Know Euler’s theorem, proof, and algorithm for Euler circuits.
Exercises 代做北美数学作业
A.Textbook Questions
10.4 Exercises 1ad.
9.5 Exercises 1, 2.
11.1 Exercises 2.
11.3 Exercises 18, 20a.
For 11.3 Exercise 18 use proof by induction on the length of the path.
For exercise 20 don’t give the answer in the book. Instead, start with the cycle
a → d → h → i → f → b → a.
Now apply the proof of Euler’s theorem to remove this cycle from the graph. You will get a graph with one connected component. Construct an Euler circuit for it then join it to the cycle to get an Euler circuit for the graph.
B.Instructor Questions 代做北美数学作业
Questions on 10.4
1.Consider the recurrence an = an-1 + n − 1 with a1 = 0.
(a) Determine a0, a2, a3 and a4.
(b) Use the method of 10.4 to fifind the rational generating function for an.
(c) For the answer 
that you obtain in part (b) verify that
q(x)(a0 + a1x + a2x2 + a3x3 + a4x4 + . . .) = p(x)
up to x4.
2.The generating function for the Fibonacci sequence 0, 1, 1, 2, 3, 5, 8, 13, 21, . . . is
F(x) =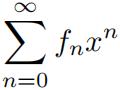
= x + x2 + 2x3 + 3x4 + 5x5 + 8x6 + . . . .
Because the Fibonacci sequence is generated by a linear recurrence fn= fn-1+ fn-2 with constant coeffificients it has a rational GF. Use the method of section 10.4 to fifind the rational generating function for fn.
Questions on 9.5
3.Show that
by induction on n.
4.Show that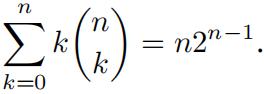
Hint: Write out 2
= ….
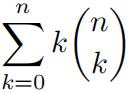Questions on 11.1
5.Suppose G is a simple graph with 10 vertices and 10 edges. What is the maximum number of connected components that G can have? How does this change if G is a multigraph? 代做北美数学作业
6.Draw the multigraph G = (V, E) where V = {1, 2, 3, 4, 5} and E = {{1, 2}, {2, 3}, {2, 3}, {3, 3}, {3, 1}, {4, 5}, {4, 5}, {4, 1}} and list all cycles in G.
7.Let G be a connected graph and e any edge in G. Prove that G − e (i.e. G with edge e removed) is connected if and only if e is in a cycle of G.
Questions on 11.3 代做北美数学作业
8.(a) Does K4 have an Euler circuit? If yes, draw one. If not, explain.
(b) Does K4 have an Euler trail? If yes, draw one. If not, explain.
(c) Does K5 have an Euler circuit? If yes, draw one. If not, explain.
(d) Does K5 have an Euler trail? If yes, draw one. If not, explain.
9.A simple graph G has 7 vertices. Can the degree of every vertex be 3? If yes draw such a graph.
If not explain.
10.Let G be a connected multigraph with exactly two vertices of odd degree. Show that G has an Euler trail.
