欢迎各位阅读本篇,Apriori算法是一种挖掘关联规则的频繁项集算法,其核心思想是通过候选集生成和情节的向下封闭检测两个阶段来挖掘频繁项集。而且算法已经被广泛的应用到商业、网络安全等各个领域。

随着大数据概念的火热,啤酒与尿布的故事广为人知。我们如何发现买啤酒的人往往也会买尿布这一规律?数据挖掘中的用于挖掘频繁项集和关联规则的Apriori算法可以告诉我们。本文首先对Apriori算法进行简介,而后进一步介绍相关的基本概念,之后详细的介绍Apriori算法的具体策略和步骤,最后给出Python实现代码。
1.Apriori算法简介
Apriori算法是经典的挖掘频繁项集和关联规则的数据挖掘算法。A priori在拉丁语中指”来自以前”。当定义问题时,通常会使用先验知识或者假设,这被称作”一个先验”(a priori)。Apriori算法的名字正是基于这样的事实:算法使用频繁项集性质的先验性质,即频繁项集的所有非空子集也一定是频繁的。Apriori算法使用一种称为逐层搜索的迭代方法,其中k项集用于探索(k+1)项集。首先,通过扫描数据库,累计每个项的计数,并收集满足最小支持度的项,找出频繁1项集的集合。该集合记为L1。然后,使用L1找出频繁2项集的集合L2,使用L2找出L3,如此下去,直到不能再找到频繁k项集。每找出一个Lk需要一次数据库的完整扫描。Apriori算法使用频繁项集的先验性质来压缩搜索空间。
2. 基本概念
项与项集:设itemset={item1, item_2, …, item_m}是所有项的集合,其中,item_k(k=1,2,…,m)成为项。项的集合称为项集(itemset),包含k个项的项集称为k项集(k-itemset)。
事务与事务集:一个事务T是一个项集,它是itemset的一个子集,每个事务均与一个唯一标识符Tid相联系。不同的事务一起组成了事务集D,它构成了关联规则发现的事务数据库。
关联规则:关联规则是形如A=>B的蕴涵式,其中A、B均为itemset的子集且均不为空集,而A交B为空。
支持度(support):关联规则的支持度定义如下:
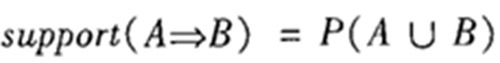
其中P(A∪B)表示事务包含集合A和B的并(即包含A和B中的每个项)的概率。注意与P(A or B)区别,后者表示事务包含A或B的概率。
置信度(confidence):关联规则的置信度定义如下:
项集的出现频度(support count):包含项集的事务数,简称为项集的频度、支持度计数或计数。
频繁项集(frequent itemset):如果项集I的相对支持度满足事先定义好的最小支持度阈值(即I的出现频度大于相应的最小出现频度(支持度计数)阈值),则I是频繁项集。
强关联规则:满足最小支持度和最小置信度的关联规则,即待挖掘的关联规则。
3. 实现步骤
一般而言,关联规则的挖掘是一个两步的过程:
找出所有的频繁项集
由频繁项集产生强关联规则
3.1挖掘频繁项集
3.1.1 相关定义
连接步骤:频繁(k-1)项集Lk-1的自身连接产生候选k项集Ck
Apriori算法假定项集中的项按照字典序排序。如果Lk-1中某两个的元素(项集)itemset1和itemset2的前(k-2)个项是相同的,则称itemset1和itemset2是可连接的。所以itemset1与itemset2连接产生的结果项集是{itemset1[1], itemset1[2], …, itemset1[k-1], itemset2[k-1]}。连接步骤包含在下文代码中的create_Ck函数中。
剪枝策略
由于存在先验性质:任何非频繁的(k-1)项集都不是频繁k项集的子集。因此,如果一个候选k项集Ck的(k-1)项子集不在Lk-1中,则该候选也不可能是频繁的,从而可以从Ck中删除,获得压缩后的Ck。下文代码中的is_apriori函数用于判断是否满足先验性质,create_Ck函数中包含剪枝步骤,即若不满足先验性质,剪枝。
删除策略
基于压缩后的Ck,扫描所有事务,对Ck中的每个项进行计数,然后删除不满足最小支持度的项,从而获得频繁k项集。删除策略包含在下文代码中的generate_Lk_by_Ck函数中。
3.1.2 步骤
每个项都是候选1项集的集合C1的成员。算法扫描所有的事务,获得每个项,生成C1(见下文代码中的create_C1函数)。然后对每个项进行计数。然后根据最小支持度从C1中删除不满足的项,从而获得频繁1项集L1。
#p#分页标题#e#
对L1的自身连接生成的集合执行剪枝策略产生候选2项集的集合C2,然后,扫描所有事务,对C2中每个项进行计数。同样的,根据最小支持度从C2中删除不满足的项,从而获得频繁2项集L2。
对L2的自身连接生成的集合执行剪枝策略产生候选3项集的集合C3,然后,扫描所有事务,对C3每个项进行计数。同样的,根据最小支持度从C3中删除不满足的项,从而获得频繁3项集L3。
以此类推,对Lk-1的自身连接生成的集合执行剪枝策略产生候选k项集Ck,然后,扫描所有事务,对Ck中的每个项进行计数。然后根据最小支持度从Ck中删除不满足的项,从而获得频繁k项集。
3.2 由频繁项集产生关联规则
一旦找出了频繁项集,就可以直接由它们产生强关联规则。产生步骤如下:
对于每个频繁项集itemset,产生itemset的所有非空子集(这些非空子集一定是频繁项集);
对于itemset的每个非空子集s,如果
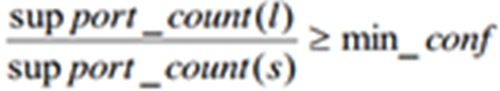
则输出s=>(l-s),其中min_conf是最小置信度阈值。
4. 样例以及Python实现代码
下图是挖掘频繁项集的样例图解。
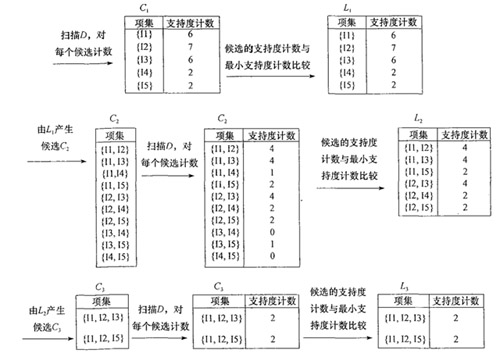
本文基于该样例的数据编写Python代码实现Apriori算法。代码需要注意如下两点:
由于Apriori算法假定项集中的项是按字典序排序的,而集合本身是无序的,所以我们在必要时需要进行set和list的转换;
由于要使用字典(support_data)记录项集的支持度,需要用项集作为key,而可变集合无法作为字典的key,因此在合适时机应将项集转为固定集合frozenset。
"""
# Python 2.7
# Filename: apriori.py
# Author: llhthinker
# Email: hangliu56[AT]gmail[DOT]com
# Blog: http://www.cnblogs.com/llhthinker/p/6719779.html
# Date: 2017-04-16
"""
def load_data_set():
"""
Load a sample data set (From Data Mining: Concepts and Techniques, 3th Edition)
Returns:
A data set: A list of transactions. Each transaction contains several items.
"""
data_set = [['l1', 'l2', 'l5'], ['l2', 'l4'], ['l2', 'l3'],
['l1', 'l2', 'l4'], ['l1', 'l3'], ['l2', 'l3'],
['l1', 'l3'], ['l1', 'l2', 'l3', 'l5'], ['l1', 'l2', 'l3']]
return data_set
def create_C1(data_set):
"""
Create frequent candidate 1-itemset C1 by scaning data set.
Args:
data_set: A list of transactions. Each transaction contains several items.
Returns:
C1: A set which contains all frequent candidate 1-itemsets
"""
C1 = set()
for t in data_set:
for item in t:
item_set = frozenset([item])
C1.add(item_set)
return C1
def is_apriori(Ck_item, Lksub1):
"""
Judge whether a frequent candidate k-itemset satisfy Apriori property.
Args:
Ck_item: a frequent candidate k-itemset in Ck which contains all frequent
candidate k-itemsets.
Lksub1: Lk-1, a set which contains all frequent candidate (k-1)-itemsets.
Returns:
True: satisfying Apriori property.
False: Not satisfying Apriori property.
"""
for item in Ck_item:
sub_Ck = Ck_item - frozenset([item])
if sub_Ck not in Lksub1:
return False
return True
def create_Ck(Lksub1, k):
"""
Create Ck, a set which contains all all frequent candidate k-itemsets
by Lk-1's own connection operation.
Args:
Lksub1: Lk-1, a set which contains all frequent candidate (k-1)-itemsets.
k: the item number of a frequent itemset.
Return:
Ck: a set which contains all all frequent candidate k-itemsets.
"""
Ck = set()
len_Lksub1 = len(Lksub1)
list_Lksub1 = list(Lksub1)
for i in range(len_Lksub1):
for j in range(1, len_Lksub1):
l1 = list(list_Lksub1[i])
l2 = list(list_Lksub1[j])
l1.sort()
l2.sort()
if l1[0:k-2] == l2[0:k-2]:
Ck_item = list_Lksub1[i] | list_Lksub1[j]
# pruning
if is_apriori(Ck_item, Lksub1):
Ck.add(Ck_item)
return Ck
def generate_Lk_by_Ck(data_set, Ck, min_support, support_data):
"""
Generate Lk by executing a delete policy from Ck.
Args:
data_set: A list of transactions. Each transaction contains several items.
Ck: A set which contains all all frequent candidate k-itemsets.
min_support: The minimum support.
support_data: A dictionary. The key is frequent itemset and the value is support.
Returns:
Lk: A set which contains all all frequent k-itemsets.
"""
Lk = set()
item_count = {}
for t in data_set:
for item in Ck:
if item.issubset(t):
if item not in item_count:
item_count[item] = 1
else:
item_count[item] += 1
t_num = float(len(data_set))
for item in item_count:
if (item_count[item] / t_num) >= min_support:
Lk.add(item)
support_data[item] = item_count[item] / t_num
return Lk
def generate_L(data_set, k, min_support):
"""
Generate all frequent itemsets.
Args:
data_set: A list of transactions. Each transaction contains several items.
k: Maximum number of items for all frequent itemsets.
min_support: The minimum support.
Returns:
L: The list of Lk.
support_data: A dictionary. The key is frequent itemset and the value is support.
"""
support_data = {}
C1 = create_C1(data_set)
L1 = generate_Lk_by_Ck(data_set, C1, min_support, support_data)
Lksub1 = L1.copy()
L = []
L.append(Lksub1)
for i in range(2, k+1):
Ci = create_Ck(Lksub1, i)
Li = generate_Lk_by_Ck(data_set, Ci, min_support, support_data)
Lksub1 = Li.copy()
L.append(Lksub1)
return L, support_data
def generate_big_rules(L, support_data, min_conf):
"""
Generate big rules from frequent itemsets.
Args:
L: The list of Lk.
support_data: A dictionary. The key is frequent itemset and the value is support.
min_conf: Minimal confidence.
Returns:
big_rule_list: A list which contains all big rules. Each big rule is represented
as a 3-tuple.
"""
big_rule_list = []
sub_set_list = []
for i in range(0, len(L)):
for freq_set in L[i]:
for sub_set in sub_set_list:
if sub_set.issubset(freq_set):
conf = support_data[freq_set] / support_data[freq_set - sub_set]
big_rule = (freq_set - sub_set, sub_set, conf)
if conf >= min_conf and big_rule not in big_rule_list:
# print freq_set-sub_set, " => ", sub_set, "conf: ", conf
big_rule_list.append(big_rule)
sub_set_list.append(freq_set)
return big_rule_list
if __name__ == "__main__":
"""
Test
"""
data_set = load_data_set()
L, support_data = generate_L(data_set, k=3, min_support=0.2)
big_rules_list = generate_big_rules(L, support_data, min_conf=0.7)
for Lk in L:
print "="*50
print "frequent " + str(len(list(Lk)[0])) + "-itemsets\\t\\tsupport"
print "="*50
for freq_set in Lk:
print freq_set, support_data[freq_set]
print
print "Big Rules"
for item in big_rules_list:
print item[0], "=>", item[1], "conf: ", item[2]
代码运行结果截图如下:
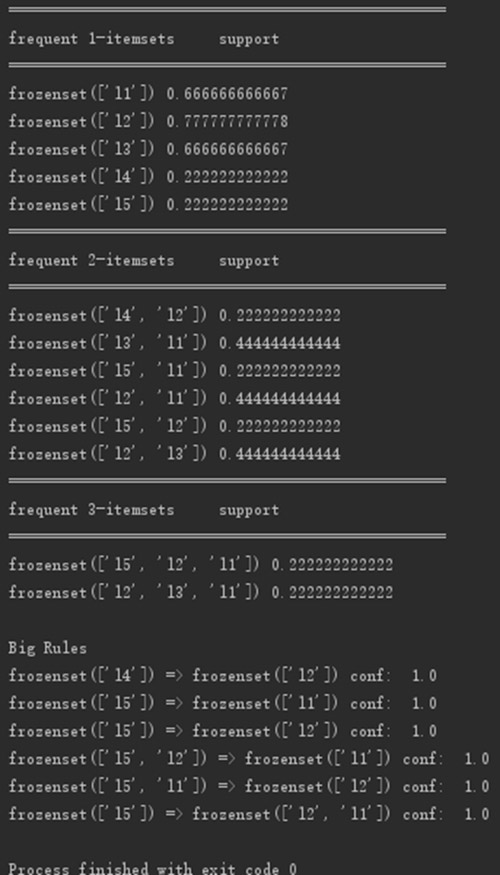
知识分享:
算法应用
#p#分页标题#e#
经典的关联规则数据挖掘算法Apriori 算法广泛应用于各种领域,通过对数据的关联性进行了分析和挖掘,挖掘出的这些信息在决策制定过程中具有重要的参考价值。
Apriori算法广泛应用于商业中,应用于消费市场价格分析中,它能够很快的求出各种产品之间的价格关系和它们之间的影响。通过数据挖掘,市场商人可以瞄准目标客户,采用个人股票行市、最新信息、特殊的市场推广活动或其他一些特殊的信息手段,从而极大地减少广告预算和增加收入。百货商场、超市和一些老字型大小的零售店也在进行数据挖掘,以便猜测这些年来顾客的消费习惯。
Apriori算法应用于网络安全领域,比如时候入侵检测技术中。早期中大型的电脑系统中都收集审计信息来建立跟踪档,这些审计跟踪的目的多是为了 性能测试或计费,因此对攻击检测提供的有用信息比较少。
它通过模式的学习和训练可以发现网络用户的异常行为模式。采用作用度的Apriori算法削弱了Apriori算法的挖掘结果规则,是网络入侵检测系统可以快速的发现用户的行为模式,能够快速的锁定攻击者,提高了基于关联规则的入侵检测系统的检测性。
Apriori算法应用于高校管理中。随着高校贫困生人数的不断增加,学校管理部门资助工作难度也越加增大。针对这一现象,提出一种基于数据挖掘算法的解决方法。
#p#分页标题#e#
将关联规则的Apriori算法应用到贫困助学体系中,并且针对经典Apriori挖掘算法存在的不足进行改进,先将事务数据库映射为一个 布尔矩阵,用一种逐层递增的思想来动态的分配内存进行存储,再利用向量求”与”运算,寻找频繁项集。实验结果表明,改进后的Apriori算法在运行效率上有了很大的提升,挖掘出的规则也可以有效地辅助学校管理部门有针对性的开展贫困助学工作。
Apriori算法被广泛应用于移动通信领域。移动增值业务逐渐成为移动通信市场上最有活力、最具潜力、最受瞩目的业务。随着产业的复苏,越来越多的增值业务表现出强劲的发展势头,呈现出应用多元化、营销品牌化、管理集中化、合作纵深化的特点。
针对这种趋势,在关联规则数据挖掘中广泛应用的Apriori算法被很多公司应用。依托某电信运营商正在建设的增值业务web数据仓库平台,对来自移动增值业务方面的调查数据进行了相关的挖掘处理,从而获得了关于用户行为特征和需求的间接反映市场动态的有用信息,这些信息在指导运营商的业务运营和辅助业务提供商的决策制定等方面具有十分重要的参考价值。
