Econ3057/4438/8038 Industrial Organization
产业组织代写 1.There are two pizza stores, Donna’s Deep Dish and Pierce’sPizza Pies. They compete with each other by setting prices simultaneously.
1. 产业组织代写
There are two pizza stores, Donna’s Deep Dish and Pierce’sPizza Pies. They compete with each other by setting prices simultaneously. For simplicity, let all costs be zero. Experience or market surveys have shown that the relation between sales (Q) and price (P) for each firm is as follows:
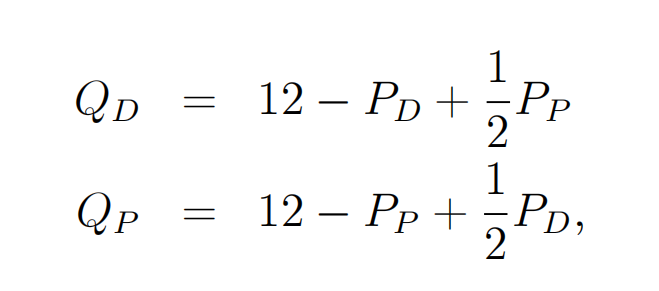
where QD and PD are the price and quantity for Donna’s Deep Dish, and QP and PP are the price and quantity for Pierce’s Pizza Pies. Note that consumers view the two products as imperfect substitutes. The demand received by one shop depends on its own price as well as the rival’s price.
(a)
If the two firms play this price setting game once, what are the equilibrium prices? What are the equilibrium profits?
(b) 产业组织代写
If the two firms work together and choose jointly the same best price, P, to maximise the sum of their profits, what is the best price? That is, the collusive price specifies the same price for both stores and maximises the sum of the two firms’ profits. What are the resulting profits per firm from collusion?
(c)
If one of them holds the price at the agreed level as in part (b), what is the best defecting price for the other firm? What are the resulting profits for the defecting firm?
(d) 产业组织代写
Now suppose the two firms play this price setting game for infinitely many periods. The two firms have the same discount factor 123 . Firms choose prices simultaneously in each period. The stage game outcome is revealed in the end of each period before firms play this stage game again in the next period. Consider the trigger strategy specifying that at the first period, firms play cooperatively according to the price calculated in part (b) until defection is observed, at which point firms revert to playing the one shot stage game Nash equilibrium forever. Find the minimum discount factor required to sustain the collusive price in part (b) by using this trigger strategy.
(e)
Now suppose that the two firms instead follow a simple penal code. The simple penal code specifies that firms play cooperatively according to the price calculated in part (b) if both firms have played cooperatively so far. Upon observation of deviation, the punishment phase begins, where firms charge PN . The punishment phase lasts for one period if both firms carry out the punishment. Firms then return to the cooperative price. If any firm deviates from the punishment price PN , the punishment phase restarts and lasts for one period with the return to the cooperative phase delayed by one period. For discount factor equal to 0:5, if the game is in the beginning of a punishment phase, for any given PN , what is the profit (in terms of PN ) for deviating from the punishment price (given that the other firm is playing PN )?
(f) 产业组织代写
Continue from part (e), what is the most severe and yet credible punishment price if firms follow the simple penal code speciÖed in part (e)?
(g)
Again for discount factor equal to 0.5, can the collusive price you found in part (b) be sustained by the simple penal code with punishment price specified in part (f)? Show your work to support your answer.
(h)
Suppose now the discount factor is so low such that the collusive price in part (b) is not sustainable by using the simple penal code. Comment on how the optimal collusive price given the penal code structure can be found in this case. [You do not need to calculate the price.]
2. 产业组织代写
Two firms offer homogenous products with demand curve
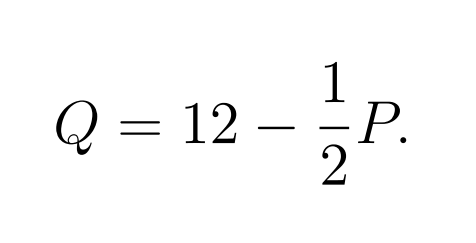
Firms compete by setting prices simultaneouly. Firms share the market equally if they charge the same price. In each period, there are two possible states of nature for the demand. With probability , there is no demand. With probability 1 , there is positive demand as specified in the demand curve. The unobservable demand shock is independent and identically distributed. The stage game is repeated infinitely. While a firm observes its own demand ex post, it does not observe the other firm’s price.
To sustain collusion, firms follow the following strategy: in the collusive phase, all firms charge the industry monopoly price, until at least one firm makes zero profit. The realisation of zero profit for at least one firm triggers the punishment phase in which both firms charge p = 0 for exactly T periods. At the end of the punishment phase (if any), the firms revert to the collusive phase. The game starts with the collusive phase. Let V+ denote the present discounted value of a firm’s profit from any given date t on, assuming that at date t the game is in the collusive
phase. Let V– denote the present discounted value of a firm’s profit from date t on, assuming that at date t the game is in the beginning of a punishment phase.
(a) 产业组织代写
Write down and solve for the expressions of V+ and V– .
(b)
Write down the incentive constraint for collusion to be sustained.
(c)
Set up the constrained optimisation problem for the firms. Comment on how to solve for the optimal punishment duration. [You do not have to solve it.]
(d)
For collusion games in general, the antitrust authority claims “If we observe aggressive pricing or output behaviour in the industry, firms must be competing with each other. Collusion is thus not a concern.” Comment on this statement if we have models with full information and observability (such as in Question 1). How would your answer change, if at all, if we have unobservable demand shocks, and firms cannot directly monitor the rivals’ behaviour (such as the set up in this question)? Explain.
Brief answer: The statement is true for models in Q1 with perfect information. Not true with imperfect monitoring.

更多代写:计算机Project代写 GMAT代考 英国MATH数学作业代写 mediaessay代写 爱尔兰媒体论文代写范文 代写JAVA设计
