ECON 3101 – Intermediate Microeconomics
Final Exam
中级微观经济学代写 2.(POINTS: 15)Imagine you are an economist hired by a firm to evaluate the tractability of a business opportunity.
1.(POINTS: 10)
Find all the Nash equilibrium of the following NFG:

2.(POINTS: 15) 中级微观经济学代写
Imagine you are an economist hired by a firm to evaluate the tractability of a business opportunity. This firm is deciding whether to accept a government proposal to start the production of a drug to treat a certain disease, the government will guarantee monopoly profits for the firm in the market during the first year, but from the second year onwards the market will be open to any firm, and players will act competitively, or to reject it which means a gain of zero.

(a) obtain the equilibrium quantity and price under the monopoly case, and calculate the monopoly profits for the first year; (Points: 6/15)
(b) calculate equilibrium price and quantity, and profits, when the firm acts competitively; (Points: 6/15)
Suppose to start production the fifirm needs to incur in a certain cost C, yet to be calculated.
(c) What is the maximum value for C your firm is willing to incur in order not to reject the proposal? Explain your answer. (for simplicity, you can assume the value of money across time is negligibly). (Points: 3/15)
3.(POINTS: 25) 中级微观经济学代写
Consider the following NFG:

Let the strategies for Country 1 be
- m for missile, e for escalate, a for acquiesce, and n for not act; and the strategies for Country 2 be
- N for not act, B for blockade, and A for attack.
(a) Find all the Nash equilibrium in pure strategies in the previous game. (Points: 7.5/25)
Now, consider the extensive formulation of the previous game:
N1 at the fifirst node, Country 1 decides m or n;
– if Country 1 n, end of the game and payoffs (4,3);
– if country 1 m, they move to node two;
N2 at node two, Country 2 decides N, B, or A;
∗ if Country 2 N, end of the game and payoffs (5,2);
∗ if Country 2 B, they move to node three;
N3 at node three, Country 1 decides e or a;
- if Country 1 e, end of the game and payoffs (0,1);
- if Country 1 a, end of the game and payoffs (3,5);
∗ if Country 2 A, they move to node four;
N4 at node four, Country 1 decides e or a;
- if Country 1 e, end of the game and payoffs (1,0);
- if Country 1 a, end of the game and payoffs (2,4);
Given the extensive formulation above:
(b) Draw the tree that represents this game and remember to
- label every node and point which player plays in which;
- identify all the branches at each node;
- associate the payoffs to each corresponding final node.
(Points: 10/25)
(c) Use backwards induction to obtain the subgame perfect equilibrium and use it to explain why a public statement from Country 2 saying that they will not react (N) to Country 1 installing missiles (m) is not a “credible threat”. (Points: 7.5/25)
4.(POINTS: 20) 中级微观经济学代写
Suppose an environment where fifirms that are competing according to Bertrand competition.
The market demand is
QD(p) = 300−2p
Assume firms have no capacity constraints. Two firms are competing in this market with cost functions
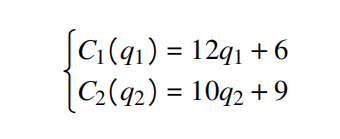
(a) Calculate the equilibrium quantities and the market price. (Points: 5/20)
Assume a new firm enters this market with a cost function
C3(q3) = 5q3 +12
(b) Calculate the new equilibrium quantities and the market price. (Points: 5/20)
Assume a fourth firm enters this market with a cost function
C4(q4) = 5q4 +20
(c) Calculate the new equilibrium quantities and the market price. (Points: 5/20)
(d) Explain why, even though only two firms sell in the market above, the market power disappears. (Points: 5/20)
5.(POINTS: 15)
Consider the following sequential direction game with 3 players. Player 1 (P1) can choose up (U) or down (D), Player 2 (P2) can choose front (F) or back (B), and Player 3 (P3) can left (L) or right (R). The game and all relevant elements are illustrated below.
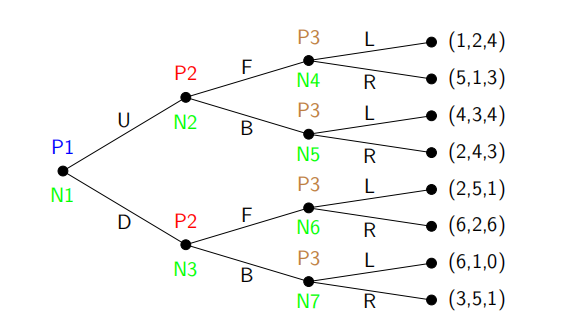
(a) How many subgames are there in the sequential game above? For each subgame you found, list all the nodes within it (e.g., subgame N4, (1,2,4), (5,1,3)) or clearly mark it in the figure above (identify each subgame). (Points: 5/15)
(b) Using backward induction, find the subgame perfect equilibrium of this game. Denote the action taken and by which player at each node (e.g., N2: P2 chooses front). (Points: 5/15)
(c) Is the subgame perfect equilibrium Pareto optimal? If yes, explain how you know. If no, which payoff Pareto dominates it?. (Points: 5/15)
6.(POINTS: 10) 中级微观经济学代写
Consider the following NFG:

(a) Use IESDS to obtain the reduced game (remember, you should stop eliminating strategies when there is no more strictly dominated ones). (Points: 5/10)
(b) Use IEDS (you can eliminate either weakly dominated strategies as well) to show that not only the order of elimination matters, but that the outcome may be different than the one obtained using IESDS. (Points: 5/10)
7.(POINTS: 20)
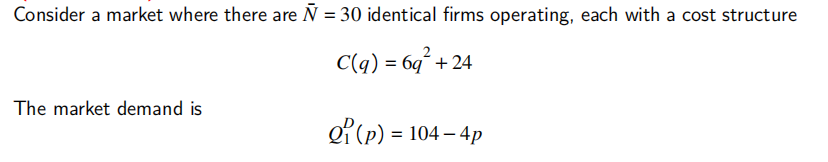
(a) Calculate the aggregate quantity and price, and individual firm’s supply and profit in the short run. (Points: 4/20)
(b) Assuming free entry and exit, calculate the aggregate quantity, price and number of firms, and each firm’s supply and profit in the long run. (Points: 4/20)

(c) Calculate the new aggregate quantity and price, and individual firm’s supply and profit in the short run. (Points: 4/20)
(d) Assuming free entry and exit, calculate the new aggregate quantity, price and number of firms, and each firm’s supply and profit in the long run. (Points: 4/20)
(e) Draw a qp-diagram and represent the short run supply curve for each case, the long run supply, and the two market demands. Do not forget to plot the short run and long run equilibria. (Points: 4/20)
8.(POINTS: 15) 中级微观经济学代写
Imagine a market where a monopolist can price discriminate between two groups. The inverse demand function for group 1 is
P1(q1) = 36−3q1
and the inverse demand function for group 2 is
P2(q2) = 34−2q2
The cost function for the monopolist is
C(q) = 6q+10
where q = q1 +q2.
(a) Solve the profit maximization problem for this price discriminating monopolist and compute the equilibrium quantity and price for each market, as well as the total profit obtained by the monopolist. (Points: 10/15)
Now, suppose this monopolist can perfectly discriminate within each market.
(b) Obtain the whole profit for the monopolist, and compare it to the profit obtained in the previous item. Explain. (Points: 5/15)
9.(POINTS: 20) 中级微观经济学代写

(a) Set the profit maximization profit for each firm, and find their best response function. (Points: 5/20)
(b) Solve for the Cournot outcome for each firm, calculate the equilibrium price, and obtain each firm’s profit. (Points: 5/20)
(c) Plot on a q1q2-diagram the best response for each firm and mark the point that represents the Cournot outcome. (Points: 5/20)
At this point, assume firms are now competing on a Stackelberg framework and assume firm 1 is the first mover.
(d) Calculate the Stackelberg equilibrium (quantities, price and firms’ profits) and explain what is the first-mover advantage by comparing your results. (Points: 5/20)

更多代写:程序编程代考 GMAT代考 英国材料科学代写ASSIGNMENT 代写Essay英国 毕业论文Results代写 西沃恩南方大学代写
