IEOR 3609: Advanced Optimization
Sample Midterm
高级优化考试代考 Problem 1 You are planning family trips for the year. You have a list of 10 domestic destinations and 10 international destinations.
Problem 1
You are planning family trips for the year. You have a list of 10 domestic destinations and 10 international destinations. You ask each of your 12 family members to pick one domestic destination and one international destination from this list. Find the smallest set of destinations such that for each family member, at least one of his/her picks is included in this subset.
(a) Formulate this problem as an integer program.
(b) Argue that your formulation in (a) satisfies total unimodularity. (if needed, reformulate the IP to make sure it does satisfy total unimodularity)
Problem 2 高级优化考试代考
A salesman needs to visit n cities in a given order: C1, C2, . . . , Cn, starting from city C0. The salesman can travel for at most 20 hours in one day. It takes hi hours go from Ci−1 to Ci , where hi is an integer and hi ≤ 20, for all i = 1, . . . , n. Break this tour into multiple days, so that each day, the salesman travels for 20 hours or less. (You cannot end a day’s travel at some point between two cities. That is, for any i, if you start the leg Ci−1 → Ci on a day, you must completely finish it on the same day.)
Consider the following greedy heuristic for breaking the tour: travel as much as possible on the first day, then as much as possible on second day, and so on. For each of the three criteria (a), (b), and (c) below, either prove that this greedy heuristic is optimal or give a counter example.
(a) Minimize the number of travel days 高级优化考试代考
(b) After finishing a day’s travel, the salesman spends the remaining hours of the day at a hotel, which charges per hour. Minimize the total number of hours spent in a hotel on all but the last day.
(c) Minimize the maximum of the number of hours spent in a hotel on all but the last day.
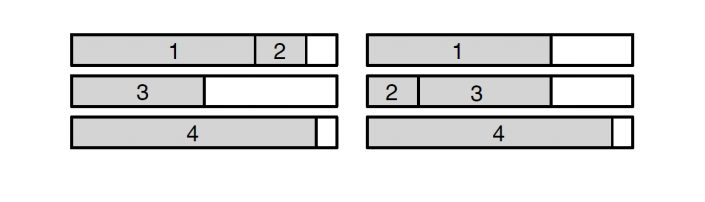
Below is an example. Here, a tour of 4 cities has been broken into 3 days in two possible ways. The shaded part shows the hours of the day spent traveling, and the white part shows the hours spent in a hotel. So, in the first case, the salesman covers the first two legs C0 → C1 → C2 on the first day, third leg C2 → C3 on the second day, and the fourth leg C3 → C4 on the last day. The total number of hours spent in the hotel are same for both cases. However, on the third criteria, i.e., the maximum of the number of hours spent, the second way of breaking the tour is better than the first.
Problem 3 高级优化考试代考
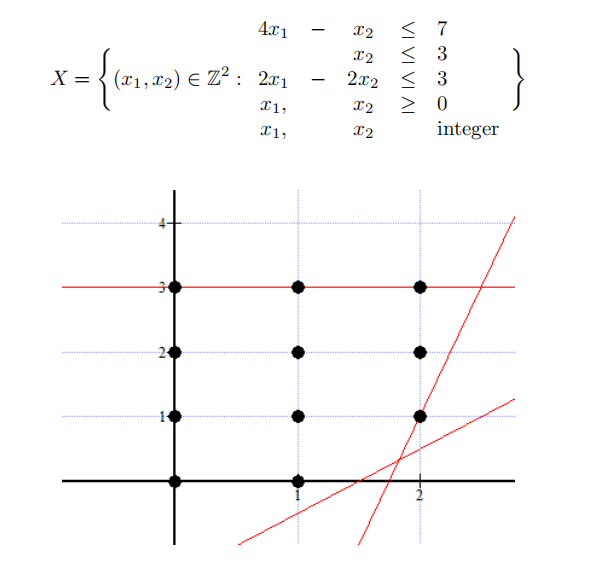
Given the set X below, find two valid inequalities such that if X’ denotes the new set defined by adding these inequalities to the set X, then the LP relaxation of X’ is equal to the convex hull of X. Derive each of these valid inequalities from the given inequalities in X, using Ch´vatal-Gomory procedure.
Problem 4 高级优化考试代考
Consider the following integer program:
max −x1 + 2x2
subject to: −4x1 + 6x2 + x3 = 9
x1 + x2 + x4 = 4
x1, x2, x3, x4 ≥ 0
x1, x2, x3, x4 integer
On solving the LP relaxation, the following simplex tableaux is obtained:
x1 − 0.1x3 + 0.6x4 = 1.5
x2 + 0.1x3 + 0.4x4 = 2.5
Use Ch´vatal-Gomory procedure to derive two valid inequalities that are not satisfied by the current LP solution (1.5, 2.5, 0, 0).

更多代写:cs台湾网课代修 托福代考 英国人权Assignment代写 商科essay论文代写 日语论文代写价格 代写sci论文
