Introduction to Electrical and Electronic Engineering
Final Exam
电气与电子工程考试代写 QUESTION 1The Sydney Light Rail is supplied with power by substations which are located 10 km apart. Each of these substations maintains a
Exam Technique
Planning your time is vital. Read the entire question paper before embarking on ANY solution.
Take your time to prioritise the questions, which can be attempted in ANY order.
Start with the question you are most confident with, and leave questions that require more thought to last.
Make a rough estimate of the time you would like to work on a problem, taking into account your knowledge of the material and the expectations of the question. Your time may not necessarily be divided evenly between questions. Stick to your allotted time – there is nothing worse than “knowing how to do something” and not having the time to write it down to demonstrate it.
QUESTION 1 电气与电子工程考试代写
The Sydney Light Rail is supplied with power by substations which are located 10 km apart. Each of these substations maintains a constant voltage between trolley wire and track of 3.3 kV at the substations. The trolley wire has a resistance of 180 mΩ/km and the rails have an equivalent resistance of 30 mΩ/km.
Two trams are in the section between two substations A and B as shown in the figure:
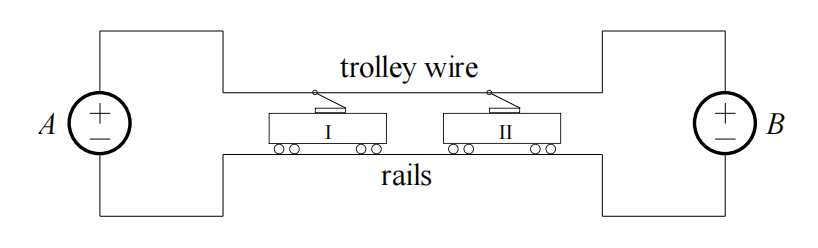
One tram is 2.5 km from substation A and draws a current of 185 A. The other tram is 3.5 km from substation B and draws a current of 315 A.
(i) Show that the current drawn from each substation is:
IA = 249 A IB = 251A
(ii) Determine the voltage across each tram.
(iii) Determine the resistance of each tram.
(iv) Calculate the total power supplied by the two substations.
(v) Calculate the total power delivered to the two trams.
QUESTION 2 电气与电子工程考试代写
A generator, Vg = 100VRMS, supplies power to a load which is connected between terminals A and B in the circuit below.
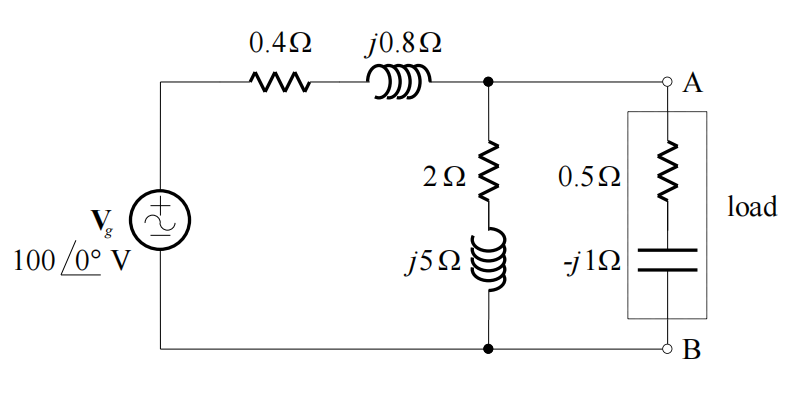
(i) Show that the current in the load, expressed as a phasor, is:
IL = 96.33∠21.02°A
(ii) Show that the load voltage between terminals A and B is given by the phasor:
VL =107.7∠- 42.41°V
(iii) Calculate the real and reactive power in the load.
(iv) Determine the required resistance and reactance of the load for maximum power transfer.
QUESTION 3 电气与电子工程考试代写
(a) State Gauss’ Law and illustrate it by a simple example.
(b) A cylindrical co-axial cable has an inner conductor of radius a and an outer conductor of radius b. The space between the conductors is filled with a dielectric of relative permittivity er = 1 .
Assume a uniform charge density of l Cm-1 on the inner conductor.
Assume the cable is so long that end effects can be neglected.
(i) Sketch the electric field distribution in the space between the conductors.
(ii) Use Gauss’ Law to find an expression for the electric flux density (D) and electric field intensity (E) at a radius r between a and b.
(iii) Find an expression for the capacitance per unit length of cable, and explain your reasoning.
(iv) How would flux density, field intensity, and capacitance be affected if the space between the conductors were filled with a dielectric of relative permittivity er = 2 ?
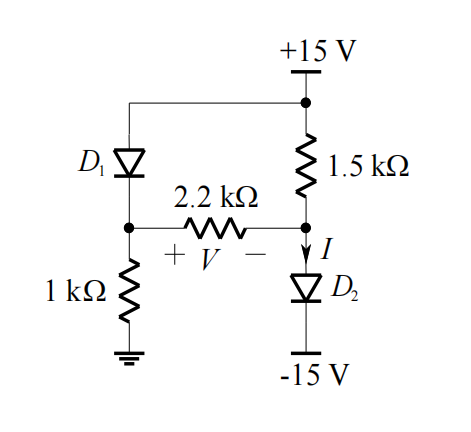
QUESTION 4

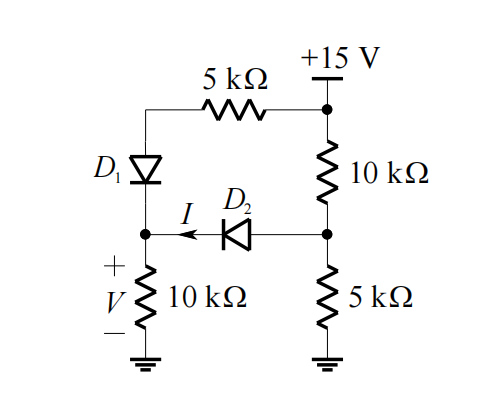
(b) Find the values of I and V for the circuit below, assuming that the diodes are ideal.
QUESTION 5
Consider the circuit shown below:
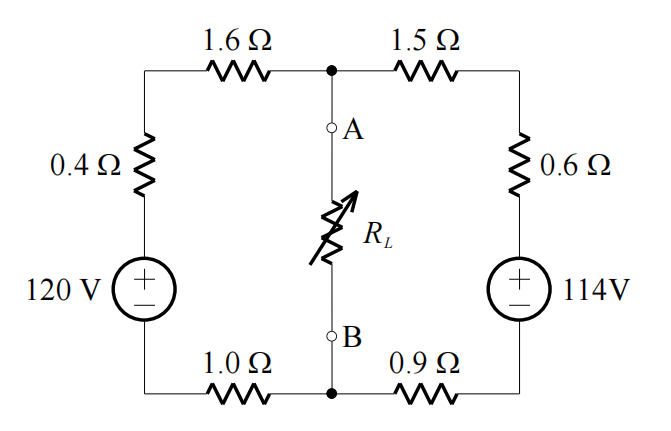
(i) Determine the Thévenin equivalent circuit from the perspective of terminals A and B.
(ii) Determine the maximum power which can be dissipated in RL and the value of RL to give this maximum power.
(iii) Determine the maximum voltage obtainable across RL and the value of RL to give this voltage.
(iv) Determine the current in a short circuit between terminals A and B.
(v) Determine the value(s) of RL if RL dissipates 1 kW of power.
QUESTION 6
In the circuit shown in the figure, the total power is 4.8 kW and the voltage measured across the resistance is 115 V RMS.
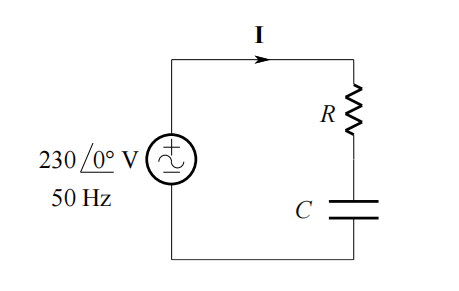
(i) Determine the current , expressed as a phasor.
(ii) Determine the impedance Z of the circuit.
(iii) Determine the resistance R and the capacitance C.
(iv) Determine the power factor of the circuit.
(v) Sketch the supply voltage and current as a function of time.
QUESTION 7 电气与电子工程考试代写
(a)
(i) Explain why, in an electrostatic field, flux lines must cross equipotentials at right
angles.
(ii) What is meant by a tube of flux? Explain what surfaces form its boundaries, and
give one of its basic properties. Sketch part of a typical electrostatic field distribution and identify within it a tube of flux.
(b) A toroidal coil has a mean radius r, a circular winding cross-section A, and a total of N turns uniformly distributed and carrying a current I.
(i) Derive the magnetic flux density along the (circular) axis of the toroid from first
principles, assuming the coil is in air. Explain every step of the derivation.
(ii) How would the flux density be affected if the core of the toroid were an iron ring of cross-section A and relative permeability mr =1000 ?
Note:μ0 = 4π×10–7 Hm-1 .
QUESTION 8 电气与电子工程考试代写
Given the following truth table:
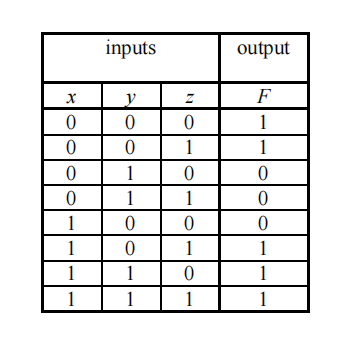
(i) Simplify the function F to a minimum number of literals.
(ii) Draw a logic circuit that generates F that is implemented entirely with 2-input NAND gates.
(b) Find the values of I and V for the circuit below, assuming that the diodes are ideal.

更多代写:计算机labreport代考 多邻国代考 英国社会学sociology代写 商科网课essay代写 商业伦理学英文论文代写 论文开题报告代写
