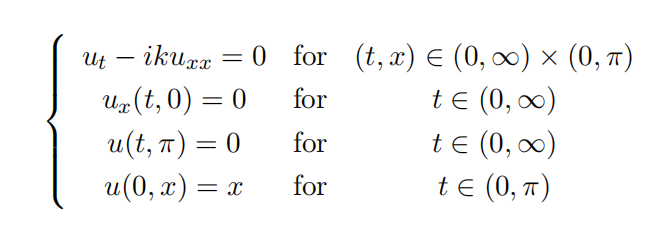Math 3FF3 – Practice Exam
The Classical Partial Diferential Equations
偏微分方程代写 Give full solutions to each of the following problems. Remember that you will be marked for the clarity and accuracy of your work,
Give full solutions to each of the following problems. Remember that you will be marked for the clarity and accuracy of your work, not just correctness. You will have plenty of time on the test, so take as much time as you need to make sure that your reasoning can be clearly understood by the reader.
1. 偏微分方程代写
Suppose that h(t) is twice difffferentiable with h(0) = 0 and conisder the initial value problem
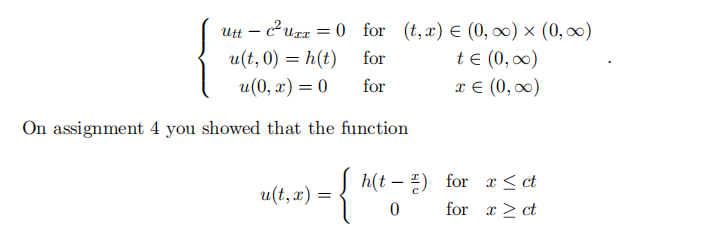
is a solution to the IVP given the assumption that h‘(0) = h”(0) = 0. Now show that this assumption is necessary, i.e. construct a function h(t) with h‘(0) ≠ 0 or h”(0) ≠ 0 such that u(t, x) is not a solution to the IVP.
2.
Solve the boundary value problem given by
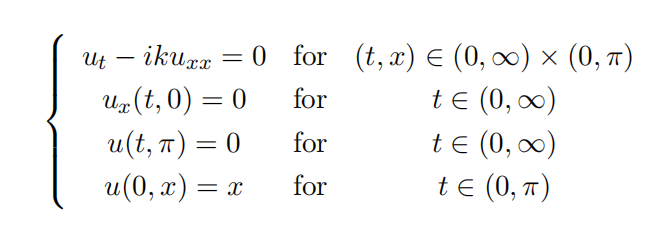
where i is the complex unit and k∈ R . Be sure to include enough explanation that the logic of your computation is clear.
3. 偏微分方程代写
State the defifinitions of pointwise convergence, uniform convergence, and mean-square convergence.
(a) Explain (with justifification) the implications between these three defifinitions, i.e. which of these properties imply which others.
(b) For each implication in your answer to (a), give an example of a sequence of functions on the interval (0, 1) which satisfy one defifintion but not the other.
(c) Explain the signifificance of mean-square convergence with regard to our study of Fourier series.
4.
Write out the proof of uniqueness in Theorem 7 of the Lecture Notes that uses Green’s formula as described on page 83-84 of the Lecture Notes, but with much more detail than is given in the Lecture Notes. You are invited to include the argument from the Lecture Notes, but you will be marked on what you add to the proof.
5. 偏微分方程代写
Solve the inhomogeneous initial value problem given by
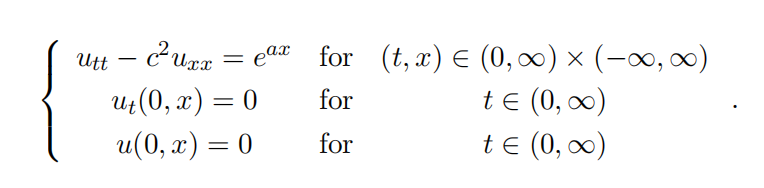
where a ∈ R. Be sure to include enough explanation that the logic of your computation is clear.
6.
Suppose that u(t, x) is a solution to the difffferential equation ut = kuxx for all t > 0, x ∈ R, where k is a fifixed real number.
(a) Prove that the translate u(t, x − x0) is also a solution for any x0 ∈ R.
(b) Prove that any derivative (e.g. ux, utt, etc.) of u is also a solution. You may assume that the derivatives exist and are continuous.

更多代写:英国前端代写 Philosophy代考 英国econ Midterm代考 Comparative Essay代写 report论文写作 操作系统考试代写